已知曲线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程
的极坐标方程 .
.
(Ⅰ)将曲线 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)曲线 ,
, 是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
在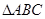 中,内角
中,内角 的对边分别为
的对边分别为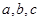 ,且
,且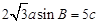 ,
, .
.
(1)求角 的大小;(2)设
的大小;(2)设 边的中点为
边的中点为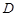 ,
,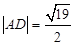 ,求
,求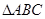 的面积.
的面积.
已知函数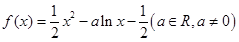
(1)当a=2时,求曲线y=f(x) 在点(1,f(1)) 处的切线方程;
(2)求函数f(x)的单调区间;
(3)若对任意的x∈[1,+∞),都有f(x)≥0成立,求a的取值范围.
某化工厂引进一条先进的生产线生产某种化工产品,其生产的总成本 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为 ,已知此生产线年产量最大为210吨,
,已知此生产线年产量最大为210吨,
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF= BD.
BD.
(1)求证:BF∥平面ACE;
(2)求证:平面EAC⊥平面BDEF
(3)求几何体ABCDEF的体积.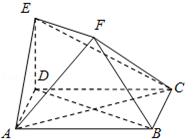
如图所示茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.
(1)若甲、乙两个小组的数学平均成绩相同,求a的值;
(2)求乙组平均成绩超过甲组平均成绩的概率;
(3)当a=2时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.