已知
.
(Ⅰ) 若不等式
在区间
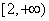上恒成立，求实数
的取值范围;
(Ⅱ) 解关于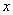
的不等式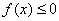
.
如图所示，在三棱柱ABCA1B1C1中，M、N分别是BC和A1B1的中点．求证：MN∥平面AA1C1.
如图，在三棱柱ABC－A1B1C1中，D是BC的中点．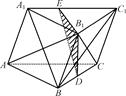
(1)若E为A1C1的中点，求证：DE∥平面ABB1A1；
(2)若E为A1C1上一点，且A1B∥平面B1DE，求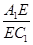
的值．.
正三棱柱ABCA1B1C1中，已知AB＝A1A，D为C1C的中点，O为A1B与AB1的交点．
(1)求证：AB1⊥平面A1BD；
(2)若点E为AO的中点，求证：EC∥平面A1BD.
如图所示，在直三棱柱ABCA1B1C1中，D、E分别为AA1、CC1的中点，AC⊥BE，点F在线段AB上，且AB＝4AF.若M为线段BE上一点，试确定M在线段BE上的位置，使得C1D∥平面B1FM.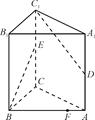
已知：a、b、c、d是不共点且两两相交的四条直线，求证：a、b、c、d共面