在极坐标系中,曲线 的极坐标方程为
的极坐标方程为 ,现以极点
,现以极点 为原点,极轴为
为原点,极轴为 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数)
为参数)
(1)写出直线l和曲线C的普通方程;
(2)设直线l和曲线C交于A,B两点,定点P(—2,—3),求|PA|·|PB|的值.
(本题14分)设
(1)当 时,求
时,求 在
在 处的切线方程;
处的切线方程;
(2)当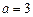 时,求
时,求 的极值;
的极值;
(3)当 时,求
时,求 的最小值。
的最小值。
(本题13分)已知函数
(1)已知一直线 经过原点
经过原点 且与曲线
且与曲线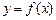 相切,求
相切,求 的直线方程;
的直线方程;
(2)若关于 的方程
的方程 有两个不等的实根,求实数
有两个不等的实根,求实数 的取值范围。
的取值范围。
(本题12分)某鲜花店每天以每束2.5元购入新鲜玫瑰花并以每束5元的价格销售,店主根据以往的销售统计得到每天能以此价格售出的玫瑰花数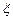 的分布列如表所示。若某天所购进的玫瑰花未售完,则当天未售出的玫瑰花将以每束1.5元的价格降价处理完毕。
的分布列如表所示。若某天所购进的玫瑰花未售完,则当天未售出的玫瑰花将以每束1.5元的价格降价处理完毕。
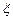 |
30 |
40 |
50 |
| P |
 |
 |
 |
(1)若某天店主购入玫瑰花40束,试求该天从玫瑰花销售中所获利润的期望;
(2)店主每天玫瑰花的进货量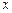
 ,单位:束
,单位:束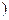 为多少时,其有望从玫瑰花销售中获得最大利润?
为多少时,其有望从玫瑰花销售中获得最大利润?
(本题12分)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
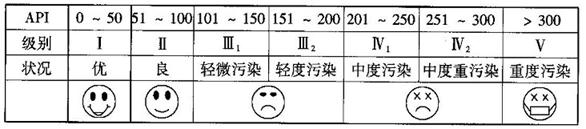
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间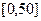 ,
,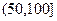 ,
,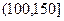 ,
, ,
,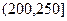 ,
,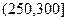 进行分组,得到频率分布直方图如图.
进行分组,得到频率分布直方图如图.
(1)求直方图中 的值;
的值;
(2)计算一年中空气质量为良的天数;
(3)某环保部门准备在一年内随机到该城市考察两次空气质量,求两次考察空气质量都为良的概率(结果用分数表示).
(本题12分)定义在R上的函数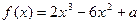 ,已知
,已知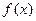 在
在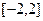 上有最小值3。
上有最小值3。
(1)求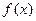 的单调区间;
的单调区间;
(2)求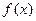 在
在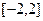 上的最大值。
上的最大值。