(本题12分)定义在R上的函数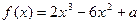 ,已知
,已知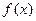 在
在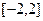 上有最小值3。
上有最小值3。
(1)求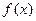 的单调区间;
的单调区间;
(2)求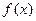 在
在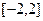 上的最大值。
上的最大值。
(本小题满分13分)已知 是腰长为2的等腰直角三角形(如图1),
是腰长为2的等腰直角三角形(如图1), ,在边
,在边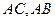 上分别取点
上分别取点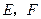 ,使得
,使得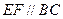 ,把
,把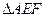 沿直线
沿直线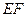 折起,使
折起,使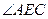 =90°,得四棱锥
=90°,得四棱锥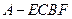 (如图2).在四棱锥
(如图2).在四棱锥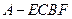 中,
中,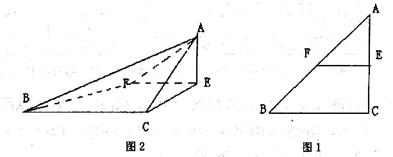
 (I)求证:CE⊥AF;
(I)求证:CE⊥AF;  (II)当
(II)当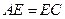 时,试在
时,试在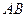 上确定一点G,使得
上确定一点G,使得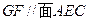 ,并证明你的结论.
,并证明你的结论.




设函数f(x) =" lnx" +ln(2-x)+ ax (a>0).
(1)当a = 1时,求f(x)的单调区间;
(2)若f(x)在(0,1]上的最大值为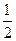 ,求a的值.
,求a的值.
用数学归纳法证明: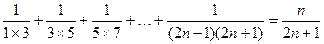 (n∈N*)
(n∈N*)
用总长14.8米的钢条制作一个长方体容器的框架,如果所制容器底面一边的长比另一边的长多0.5米,那么高为多少时容器的容积最大?最大容积是多少?
求由曲线y =" x2" 与 y =" 2-" x2 围成的平面图形的面积