如图，在△ABC中，CD是∠ACB的角平分线，△ADC的外接圆交BC于点E，AB=2AC
（1）求证：BE=2AD；
（2）当AC=3，EC=6时，求AD的长．
已知函数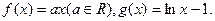
（1）若函数
存在单调递减区间，求a的取值范围；
（2）当a>0时，试讨论这两个函数图象的交点个数．
（本小题满分12分）
已知各项均为正数的数列
的前n项和
满足
（1）求数列的通项公式；
（2）设数列
为数列
的前n项和，求证：
（本小题满分12分）
如图，四棱锥P—ABCD中，底面ABCD为矩形，PD垂直于底面ABCD，AD=PD=2，
E、F分别为CD、PB的中点．
（1）求证：EF⊥平面PAB；
（2）设
求直线AC与平面AEF所成角
的正弦值．
（本小题满分12分）
袋中共有10个大小相同的编号为1、2、3的球，其中1号球有1个，2号球有m个，3号球有n个．从袋中依次摸出2个球，已知在第一次摸出3号球的前提下，再摸出一个2号球的概率是
（1）求m，n的值；
（2）从袋中任意摸出2个球，设得到小球的编号数之和为
，求随机变量的分布列和数学期望E．
（本小题满分12分）
已知向量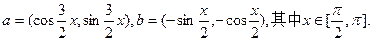
（1）若
求x的值；
（2）函数
，若
恒成立，求实数c的取值范围．