(本小题满分13分)据预测,某旅游景区游客人数在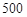 至
至 人之间,游客人数
人之间,游客人数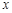 (人)与游客的消费总额
(人)与游客的消费总额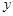 (元)之间近似地满足关系:
(元)之间近似地满足关系: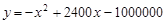
(1)若该景区游客消费总额不低于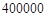 元时,求景区游客人数的范围。
元时,求景区游客人数的范围。
(2)当景区游客的人数为多少人时,游客的人均消费最高?并求游客的人均最高消费额。
(参考公式:当a>0,b>0时,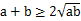 ,当且仅当a=b时等号成立)
,当且仅当a=b时等号成立)
已知向量a=(cos α,sin α),b=(cos x,sin x),c=(sin x+2sin α,cos x+2cos α),其中0<α<x<π.
(1)若α=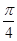 ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值;
(2)若a与b的夹角为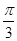 ,且a⊥c,求tan 2α的值.
,且a⊥c,求tan 2α的值.
已知函数f(x)=2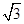 sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为
sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为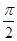 ,且点
,且点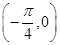 是它的一个对称中心.
是它的一个对称中心.
(1)求f(x)的表达式;
(2)若f(ax)(a>0)在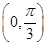 上是单调递减函数,求a的最大值.
上是单调递减函数,求a的最大值.
已知函数f(x)=2sin xcos x+2 cos2x-
cos2x- ,x∈R.
,x∈R.
(1)求函数f(x)的最小正周期;
(2)在锐角△ABC中,若f(A)=1,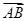 ·
·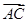 =
=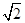 ,求△ABC的面积.
,求△ABC的面积.
设函数f(x)= +2cos2x.
+2cos2x.
(1)求f(x)的最大值,并写出使f(x)取最大值时x的集合;
(2)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(B+C)= ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
已知函数f(x)=2cos2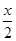 -
- sin x.
sin x.
(1)求函数f(x)的最小正周期和值域;
(2)若α为第二象限角,且f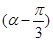 =
=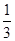 ,求
,求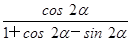 的值.
的值.