已知向量a=(cos α,sin α),b=(cos x,sin x),c=(sin x+2sin α,cos x+2cos α),其中0<α<x<π.
(1)若α=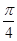 ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值;
(2)若a与b的夹角为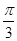 ,且a⊥c,求tan 2α的值.
,且a⊥c,求tan 2α的值.
如图,平面四边形ABCD中,AB=13,AC=10, AD=5, ,
, .
.
(Ⅰ) ;
;
(Ⅱ)设 ,求x、y的值。
,求x、y的值。
已知曲线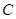 :
: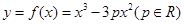 .
.
(Ⅰ)当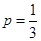 时,求曲线
时,求曲线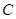 的斜率为1的切线方程;
的斜率为1的切线方程;
(Ⅱ)设斜率为 的两条直线与曲线
的两条直线与曲线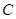 相切于
相切于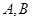 两点,求证:
两点,求证: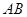 中点
中点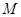 在曲线
在曲线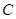 上;
上;
(Ⅲ)在(Ⅱ)的条件下,又已知直线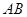 的方程为:
的方程为: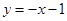 ,求
,求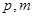 的值.
的值.
已知圆锥曲线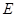 的两个焦点坐标是
的两个焦点坐标是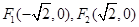 ,且离心率为
,且离心率为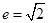 ;
;
(Ⅰ)求曲线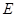 的方程;
的方程;
(Ⅱ)设曲线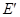 表示曲线
表示曲线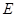 的
的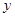 轴左边部分,若直线
轴左边部分,若直线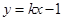 与曲线
与曲线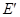 相交于
相交于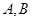 两点,求
两点,求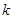 的取值范围;
的取值范围;
(Ⅲ)在条件(Ⅱ)下,如果 ,且曲线
,且曲线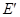 上存在点
上存在点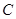 ,使
,使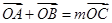 ,求
,求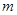 的值.
的值.
某产品具有一定的时效性,在这个时效期内,由市场调查可知,在不做广告宣传且每件获利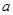 元的前提下,可卖出
元的前提下,可卖出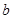 件;若做广告宣传,广告费为
件;若做广告宣传,广告费为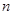 千元比广告费为
千元比广告费为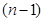 千元时多卖出
千元时多卖出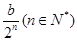 件.
件.
(Ⅰ)试写出销售量 与
与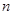 的函数关系式;
的函数关系式;
(Ⅱ)当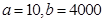 时,厂家应生产多少件这种产品,做几千元的广告,才能获利最大?
时,厂家应生产多少件这种产品,做几千元的广告,才能获利最大?
如图,四棱锥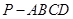 的底面
的底面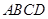 为矩形,且
为矩形,且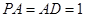 ,
, ,
,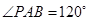 ,
, ,
,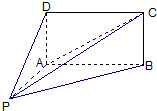
(Ⅰ)平面PAD与平面PAB是否垂直?并说明理由;
(Ⅱ)求直线PC与平面ABCD所成角的正弦值.