(本小题满分14分)若数列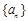 的各项均为正数,
的各项均为正数,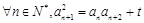 ,
,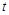 为常数,且
为常数,且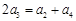 .
.
(1)求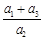 的值;
的值;
(2)证明:数列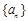 为等差数列;
为等差数列;
(3)若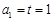 ,对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使
,对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使 ,
, ,
, 成等差数列?若存在,用k分别表示一组p和r;若不存在,请说明理由.
成等差数列?若存在,用k分别表示一组p和r;若不存在,请说明理由.
已知:如图所示,在△ABC中,AB=AC,O是△ABC的外心,延长CA到P,再延长AB
到Q,使AP=BQ.求证:O,A,P,Q四点共圆.
如图所示,圆O的两弦AB和CD交于点E,
EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.
(1)求证:△DFE∽△EFA;
(2)如果EF=1,求FG的长.
从⊙O外一点P引圆的两条切线PA,PB及一条割线PCD,A,B为切点.
求证: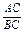 =
= .
.
已知:如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.求证:AE·BF·AB=CD3.
已知:如图所示,在△ABC中,D是BC的中点,F是BA延长线上的点,FD与AC交于点E.求证:AE·FB=EC·FA.