(本小题共13分)
如图,在直角坐标系中,O为坐标原点,直线AB⊥x轴于点C, ,动点M到直线AB的距离是它到点D的距离的2倍。
,动点M到直线AB的距离是它到点D的距离的2倍。
(I)求点M的轨迹方程;
(II)设点K为点M的轨迹与x轴正半轴的交点,直线l交点M的轨迹于E,F两点(E,F与点K不重合),且满足 ,动点P满足
,动点P满足 ,求直线KP的斜率的取值范围。
,求直线KP的斜率的取值范围。

函数 ,过曲线
,过曲线 上的点P
上的点P 的切线方程为
的切线方程为
(1)若 在
在 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)在(1)的条件下,求 在[-3,1]上的最大值;
在[-3,1]上的最大值;
(3)若函数 在区间[-2,1]上单调递增,求实数b的取值范围.
在区间[-2,1]上单调递增,求实数b的取值范围.
在数列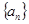 中,已知
中,已知 .
.
(Ⅰ)求数列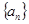 的通项公式;
的通项公式;
(Ⅱ)求证:数列 是等差数列;
是等差数列;
(Ⅲ)设数列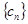 满足
满足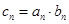 ,求
,求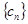 的前n项和
的前n项和 .
.
如图,在四棱锥ABCD-PGFE中,底面ABCD是直角梯形,侧棱垂直于底面,AB//DC,∠ABC=45o,DC=1,AB=2,PA=1.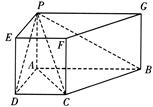
(Ⅰ)求PD与BC所成角的大小;
(Ⅱ)求证:BC⊥平面PAC;
(Ⅲ)求二面角A-PC-D的大小.
在△ABC中 ,角 、
、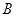 、
、 所对的边分别为
所对的边分别为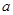 、
、 、
、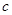 ,已知向量
,已知向量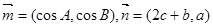 ,且
,且 .
.
(Ⅰ) 求角A的大小;
(Ⅱ) 若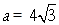 ,
, ,求△ABC的面积.
,求△ABC的面积.
某普通高中共有教师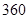 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| 第一批次 |
第二批次 |
第三批次 |
|
| 女教师 |
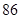 |
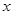 |
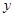 |
| 男教师 |
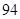 |
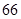 |
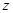 |
已知在全体教师中随机抽取1名,抽到第二、三批次中女教师的概率分别是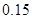 、
、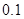 .
.
(Ⅰ)求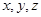 的值;
的值;
(Ⅱ)为了调查研修效果,现从三个批次中按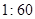 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
(Ⅲ)若从(Ⅱ)中选取的教师中随机选出两名教师进行访谈,求参加访谈的两名教师“分别来自两个批次”的概率.