如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°,且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直底面ABCD.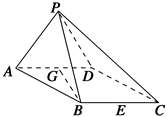
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.
(1)现要从中选派一人参加英语口语竞赛,从统计学角度,你认为派哪位学生参加更合适,请说明理由;
(2)若将频率视为概率,对学生甲在今后的三次英语口语竞赛成绩进行预测,记这三次成绩中高于80分的次数为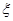 ,求
,求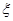 的分布列及数学期望
的分布列及数学期望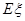 .
.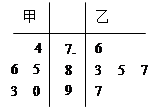
如图,四棱锥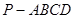 中,底面
中,底面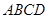 为平行四边形,
为平行四边形,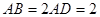 ,
,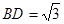 ,
, ⊥底面
⊥底面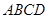 .
.
(1)证明:平面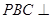 平面
平面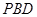 ;
;
(2)若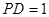 ,求
,求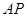 与平面
与平面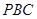 所成角
所成角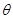 的正弦值.
的正弦值.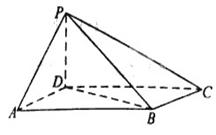
已知函数 ,数列
,数列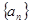 满足
满足 ,
,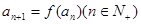
(1)求数列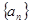 的通项公式
的通项公式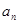 ;
;
(2)若数列 满足
满足 …+
…+ ,求
,求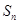
已知函数 , 其中
, 其中 ,
, ,其中
,其中 若
若 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于
(1)求 的取值范围;
的取值范围;
(2)在 中,
中, 、
、 、
、 分别是角A、B、C的对边,
分别是角A、B、C的对边, ,当
,当 最大时,
最大时, 求
求 的面积。
的面积。
在△OAB中,O为坐标原点,A(1,cosθ),B(sinθ,1) θ∈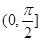 ,则△OAB的面积达到最大值时,θ=
,则△OAB的面积达到最大值时,θ=