已知:点P(m,4)在反比例函数y=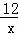 的图象上,正比例函数的图象经过点P和点Q(6,n).
的图象上,正比例函数的图象经过点P和点Q(6,n).
(1)求正比例函数的解析式;
(2)在x轴上求一点M,使△MPQ的面积等于18.
如图,在平面直角坐标系中,直线 与双曲线 交于 、 两点,已知点 ,点 .
(1)求直线和双曲线的解析式;
(2)把直线 沿 轴负方向平移2个单位后得到直线 ,直线 与双曲线 交于 、 两点,当 时,求 的取值范围.

某网络约车公司近期推出了”520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(公里),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图(如图).
|
组别 |
单次营运里程“ ”(公里) |
频数 |
|
第一组 |
|
72 |
|
第二组 |
|
|
|
第三组 |
|
26 |
|
第四组 |
|
24 |
|
第五组 |
|
30 |
根据统计表、图提供的信息,解答下面的问题:
(1)①表中 ;②样本中“单次营运里程”不超过15公里的频率为 ;③请把频数分布直方图补充完整;
(2)请估计该公司这5000个“单次营运里程”超过20公里的次数;
(3)为缓解城市交通压力,维护交通秩序,来自某市区的4名网约车司机 男1女)成立了“交通秩序维护”志愿小分队,若从该小分队中任意抽取两名司机在某一路口维护交通秩序,请用列举法(画树状图或列表)求出恰好抽到“一男一女”的概率.

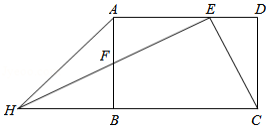
如图,点 、 分别是矩形 的边 、 上一点,若 ,且 .
(1)求证:点 为 的中点;
(2)延长 与 的延长线相交于点 ,连接 ,已知 ,求 的值.
如图,抛物线经过原点 ,点 ,点 .
(1)求抛物线解析式;
(2)连接 ,过点 作 交抛物线于 ,连接 ,求 的面积;
(3)点 是 轴右侧抛物线上一动点,连接 ,过点 作 交 轴于点 .问:是否存在点 ,使以点 , , 为顶点的三角形与(2)中的 相似,若存在,求出点 的坐标;若不存在,说明理由.

阅读下列材料:
已知:如图1,等边△ 内接于 ,点 是 上的任意一点,连接 , , ,可证: ,从而得到: 是定值.
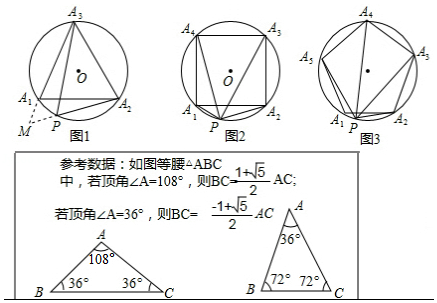
(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作 , 交 的延长线于点 .
△ 是等边三角形,
,
又 , ,
△ △

.
,是定值.
(2)延伸:如图2,把(1)中条件“等边△ ”改为“正方形 ”,其余条件不变,请问: 还是定值吗?为什么?
(3)拓展:如图3,把(1)中条件“等边△ ”改为“正五边形 ”,其余条件不变,则 (只写出结果).