如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.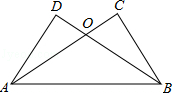
求证:(1)BC=AD;
(2)△OAB是等腰三角形.
(本小题满分12分)如图,抛物线y=Ax2+C(A≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.
(1)求此抛物线的表达式;
(2)求证:AO=AM;
(3)探究:
①当k=0时,直线y=kx与x轴重合,求出此时 的值;
的值;
②试说明无论k取何值, 的值都等于同一个常数.
的值都等于同一个常数.
(本小题满分12分)对于二次函数y=x²-3x+2和一次函数y=-2x+4,把y=t(x²-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(-1,n),请完成下列任务:
【尝试】
(1)当t=2时,抛物线y=t(x²-3x+2)+(1-t)(-2x+4)的顶点坐标为 ;
(2)判断点A是否在抛物线L上;
(3)求n的值;
【发现】
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
【应用】
二次函数 是二次函数y=x²-3x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由
是二次函数y=x²-3x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由
(本小题满分10分)某经销店为某工厂代销一种建筑材料.当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
(本小题满分10分)如图,一次函数y=kx+n的图象与x轴和y轴分别交于点A(6,0)和B(0,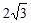 ),线段AB的垂直平分线交x轴于点C,交AB于点D.
),线段AB的垂直平分线交x轴于点C,交AB于点D.
(1)试确定这个一次函数关系式;
(2)求点C的坐标以及过A、B、C三点的抛物线的函数表达式.
(本小题满分8分)一个不透明的口袋里装有分别标有汉字“美”、“丽”、“湘”、“湖”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“湘”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用画树状图的方法,求出甲取出的两个球上的汉字恰能组成“美丽”或“湘湖”的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,再从中任取一球,记乙取出的两个球上的汉字恰能组成“美丽”或“湘湖”的概率为P2,请比较P1,P2的大小关系。