在平面直角坐标系中,A、B、C三点的坐标分别为(-6,7)、(-3,0)、(0,3).
(1)画出△ABC,则△ABC的面积为___________;
(2)在△ABC中,点C经过平移后的对应点为
C’(5,4),将△ABC作同样的平移得到△A’B’C’,
画出平移后的△A’B’C’,写出点A’,B’的坐标为
A’ (_______,_____),B’ (_______,______);
(3)P(-3,m)为△ABC中一点,将点P向右平移4个单位后,再向下平移6个单位得到点Q(n,-3),则m= ,n= .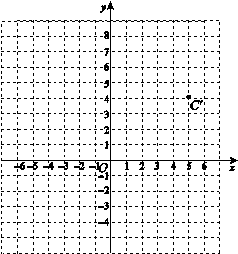
解不等式,并把解集在数轴上表示出来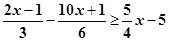
某商店出售茶壶和茶杯,茶壶每只20元,茶杯每只5元,该商店有两种优惠办法:(1)买一只茶壶送一只茶杯;(2)按总价的92%付款.现有一顾客需购买4只茶壶,茶杯若干只(不少于4只).顾客买同样多的茶杯时,选哪一种优惠办法购买最省钱?
某连队在一次执行任务中将战士编成8个组.如果每组分配人数比预定人数多1名,那么战士总数将超过100人;如果每组分配人数比预定人数少1名,那么战士总数将不到90人. 求预定每组分配战士的人数.
把一篮苹果分给几个学生,如果每人分4个,则剩3个;如果每人分6个,则最后一个学生分得的苹果不超过2个。则学生数和苹果数分别是多少?
某服装厂要生产一批某种型号的学生服装,已知3米长的布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用600米长的这种布料生产,应分别用多少布料生产上衣和裤子才能恰好配套?共能生产多少套?