(1)在Rt△ABC中,∠C=90°,∠B=30°.
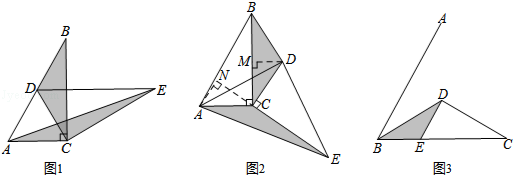
①△ABC绕点C顺时针旋转得到△DEC,点D恰好落在AB边上.如图1,则S△BDC与S△AEC的数量关系是 ;
②当△DEC绕点C旋转到图2的位置时,小娜猜想①中S△BDC与S△AEC的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小娜的猜想;
(2)已知,∠ABC=60°,点D是∠ABC平分线上一点,BD=CD=2,DE∥AB交BC于点E,如图3.若在射线BA上存在点F,使S△DCF=S△BDE,则BF= .
已知二次函数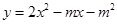 。
。
(1)求证:对于任意实数m,该二次函数图象与x轴总有公共点;
(2)若该二次函数图象与x轴有两个公共点A,B,且A点坐标为(1,0),求B点坐标。
为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE。(精确到0.1m)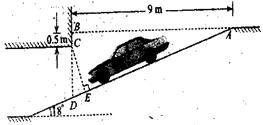
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD//CO。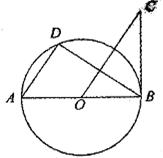
(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=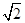 ,求AD的长。(结果保留根号)
,求AD的长。(结果保留根号)
如图,小明,小华用四张扑克牌玩游戏,他俩将扑克牌洗均匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回。
(1)若小明恰好抽到的黑桃4。
①请在右边筐中绘制这种情况的树状图;
②求小华抽出的牌的牌面数字比4大的概率。
(2)小明、小华约定:若小明抽到的牌的牌面数字比小华的大,则小明胜;反之,则小明负,你认为这个游戏是否公平?说明你的理由。
如图,平行四边形纸条ABCD中,E,F分别是边AD,BC的中点,张老师请同学将纸条的下半部分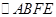 沿EF翻折,得到一个V字形图案。
沿EF翻折,得到一个V字形图案。
(1)请你在原图中画出翻折后的图形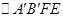 ;(用尺规作图,不写画法,保留作图痕迹)
;(用尺规作图,不写画法,保留作图痕迹)
(2)已知∠A=630,求∠B′FC的大小。