甲、乙两人进行射击训练,在相同条件下各射靶5次,成绩统计如下:
| 命中环数/环 |
7 |
8 |
9 |
10 |
| 甲命中的频数/次 |
2 |
2 |
0 |
1 |
| 乙命中的频数/次 |
1 |
3 |
1 |
0 |
(1)甲、乙两人射击成绩的极差、方差分别是多少?
(2)谁的射击成绩更稳定?
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.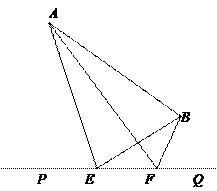
(1)判断 AB、AE的数量关系,并说明理由;
AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).
(参考数据:≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,
sin76°≈0.97,cos76°≈0.24)
如图,一次函数 的图象与反比例函数
的图象与反比例函数 的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D. 
(1) 求反比例函数 和一次函数
和一次函数 的表达式;
的表达式;
(2) 连接OA,OC.求△AOC的面积.
如图,点 的坐标为(2,
的坐标为(2, ),过点
),过点 作
作 轴的平行线交
轴的平行线交 轴于点
轴于点 ,交双曲线
,交双曲线 (
( )于点
)于点 ,作
,作 交双曲线
交双曲线 (
( )于点
)于点 ,连结
,连结 .已知
.已知 .
.
(1)求 的值.
的值.
(2)求 的周长
的周长
某中学计划对本校七年级10个班的480名学生按“学科”、“文体”、“手工”三个项目安排课外兴趣小组,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下所示的表和图.
| 兴趣小组 |
划记 |
频数 |
百分比 |
| 学科 |
正正正正正 |
25 |
|
| 文体 |
正正 |
||
| 手工 |
正正正 |
||
| 合计 |
50 |
50 |
(1)请将统计表、统计图补充完整;
(2)请以小明的统计结果来估计该校七年级480名学生参加各个项目的人数.
如图,在□ABCD中, 平分
平分 交
交 于点
于点 ,
, 平分
平分
 交
交 于点
于点 .
.
求证:(1) ;
;
(2)若 ,则判断四边形
,则判断四边形 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论.