某商店经营一种笔记本,进价为每本5元,据市场分析,在一个月内,售价定为每本8元时.可卖出105本,而售价每上涨1元,就少卖5本.
(1)设每本笔记本的售价为x元,一个月的利润为y元,写出y与x之间的函数关系式;
(2)当售价定为每本多少元时,一个月的获利最大?最大利润是多少元?
如图,在矩形 中, , ,点 为边 上的一点(与 、 不重合),四边形 关于直线 的对称图形为四边形 ,延长 交 于点 ,记四边形 的面积为 .
(1)若 ,求 的值;
(2)设 ,求 关于 的函数表达式.

有一块矩形地块 , 米, 米.为美观,拟种植不同的花卉,如图所示,将矩形 分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为 米.现决定在等腰梯形 和 中种植甲种花卉;在等腰梯形 和 中种植乙种花卉;在矩形 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元 米 、60元 米 、40元 米 ,设三种花卉的种植总成本为 元.
(1)当 时,求种植总成本 ;
(2)求种植总成本 与 的函数表达式,并写出自变量 的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120平方米,求三种花卉的最低种植总成本.

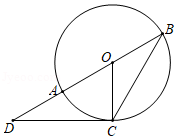
如图, 过 的圆心,交 于点 、 , 是 的切线,点 是切点,已知 , .
(1)求证: ;
(2)求 的周长.
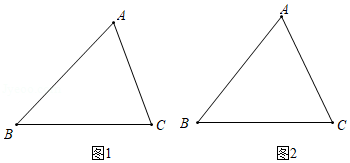
如图,已知 是锐角三角形 .
(1)请在图1中用无刻度的直尺和圆规作图:作直线 ,使 上的各点到 、 两点的距离相等;设直线 与 、 分别交于点 、 ,作一个圆,使得圆心 在线段 上,且与边 、 相切;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若 , ,则 的半径为 .
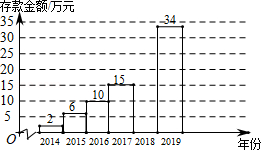
小李2014年参加工作,每年年底都把本年度收入减去支出后的余额存入银行(存款利息记入收入),2014年底到2019年底,小李的银行存款余额变化情况如下表所示:(单位:万元)
|
年份 |
2014年 |
2015年 |
2016年 |
2017年 |
2018年 |
2019年 |
|
收入 |
3 |
8 |
9 |
|
14 |
18 |
|
支出 |
1 |
4 |
5 |
6 |
|
6 |
|
存款余额 |
2 |
6 |
10 |
15 |
|
34 |
(1)表格中 ;
(2)请把下面的条形统计图补充完整;(画图后标注相应的数据)
(3)请问小李在哪一年的支出最多?支出了多少万元?