某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为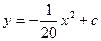 且过顶点C(0,5)(长度单位:m)
且过顶点C(0,5)(长度单位:m)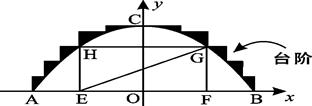
(1)直接写出c 的值;
的值;
(2)现因搞庆典活动,计 划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯,地毯的价格为20元 /
划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯,地毯的价格为20元 / 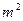 ,求购买地毯需多少元?
,求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EF GH的周长为27.5 m,求斜面EG的倾斜角∠GEF的正切值.
GH的周长为27.5 m,求斜面EG的倾斜角∠GEF的正切值.
如图所示,A、B两个旅游点从2007年至2011年“五·一”的旅游人数变化情况分别用实线和虚线表示,根据图中所示解答以下问题:
B旅游点的旅游人数相对上一年,增长最快的是哪一年?
求A、B两个旅游点从2007到2011年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价;
A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人数为4万人,为控制游客数量,A旅游点决定提高门票价格.已知门票价格x (元)与游客人数y(万人)满足函数关系y=5-.若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少?
在平面直角坐标系内,A、B、C三点的坐标分别是A(5,0)、B(0,3)、C(5,3),O 为坐标原点,点E在线段BC上,若△AEO为等腰三角形, 求点E的坐标.(画出图象,不需要写计算过程)
如图,在△ABC中,O是AC上的一个动点(不与点A、C重合),过O点作直线MN//BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F。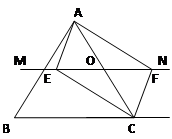
(1)试说明:OE=OF。
(2)当O点运动到何处时,四边形AECF是矩形?并证明你的结论。
如图,四边形ABCD中,AB∥CD,AC平分∠BAD ,CE∥AD交AB于点E。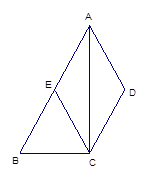
判断:四边形AECD是什么形状?并给出理由。
若点E是AB的中点,是判断△ABC的形状,并给出理由。
做图:在△ABC中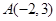 ,
,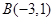 ,
,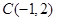 .
.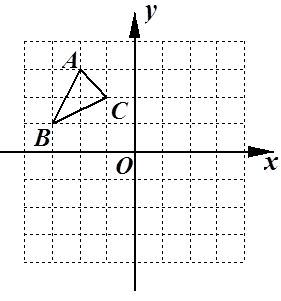
(1)将△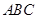 向右平移4个单位长度,画出平移后的△
向右平移4个单位长度,画出平移后的△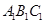 ;
;
(2)画出△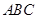 关于
关于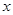 轴对称的△
轴对称的△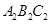 ;
;
(3)将△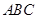 绕原点O旋转180º,画出旋转后的△
绕原点O旋转180º,画出旋转后的△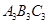 ;
;
(4)在△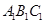 .△
.△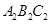 .△
.△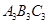 中,
中,
△ 与△ 成轴对称,对称轴是 ;
△ 与△ 成中心对称,对称中心的坐标是