如图所示，A、B两个旅游点从2007年至2011年“五·一”的旅游人数变化情况分别用实线和虚线表示,根据图中所示解答以下问题：
B旅游点的旅游人数相对上一年,增长最快的是哪一年？
求A、B两个旅游点从2007到2011年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价；
A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人数为4万人,为控制游客数量，A旅游点决定提高门票价格.已知门票价格x (元)与游客人数y（万人）满足函数关系y=5－．若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少？
一个不透明的口袋里装有红、黄、绿三种颜色的球（除颜色不同外其余都相
同），其中红球有2个，黄球有1个，从中任意摸出1个球是红球的概率为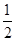
．
（1）试求袋中绿球的个数；
（2）从箱子中任意摸出一个球是黄球的概率是多少？
（3）第1次从袋中任意摸出1球（不放回），第2次再任意摸出1球，请你用画树状图
或列表格的方法，求两次都摸到红球的概率．
已知：如图是破铁轮的轮廓，请用直尺和圆规作出它的圆心。
如图1，已知抛物线y=－x2+bx+c经过点A（1,0），B（－3,0）两点，且与y轴交于点C.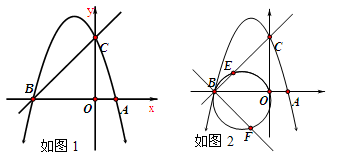
（1）求b，c的值。
（2）在第二象限的抛物线上，是否存在一点P，使得△PBC的面积最大？求出点P的坐标及△PBC的面积最大值.若不存在，请说明理由.
（3）如图2，点E为线段BC上一个动点（不与B,C重合），经过B、E、O三点的圆与过点B且垂直于BC的直线交于点F，当△OEF面积取得最小值时，求点E坐标．
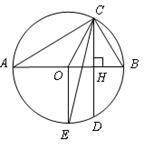
如图，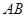
为⊙O的直径，
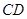为弦，且
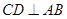，垂足为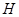
．
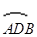（1）如果⊙O的半径为4，
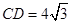，求
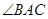的度数；
（2）若点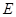
为的中点，连结
，
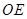．求证：平分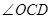
；
（3）在（1）的条件下，圆周上到直线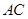
距离为3的点有多少个？并说明理由．
正方形网格中，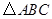
为格点三角形（顶点都是格点），将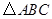绕点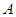
按逆时针方向旋转
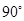得到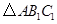
．
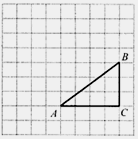
（1）在正方形网格中，作出；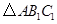
（2）设网格小正方形的边长为1，求旋转过程中动点B经过的路线长和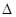
AC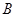
所扫过的面积．