在平面直角坐标系xOy(如图)中,已知A(﹣1,3),B(2,n)两点在二次函数y=﹣ x2+bx+4的图象上.
x2+bx+4的图象上.
(1)求b与n的值;
(2)联结OA、OB、AB,求△AOB的面积;
(3)若点P(不与点A重合)在题目中给出的二次函数的图象上,且∠POB=45°,求点P的坐标.
已知:如图,AB=3,AC=4,AB⊥AC,BD=12,CD=13,(1)求BC的长度;(2)证明:BC⊥BD.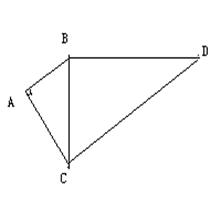
一天中国鱼政311号船在执行维权护于鱼任务时.发现在其所处的位置O点的正北方向10海里处的A点,有一走外国鱼船只正以24海里/时的速度向正东方向航行.为迅速实施拦截, 311号船调整好航向,以26海里/时的速度追赶,在不改变行速和航向的前提下.问需要最少几小时才能追上?
(10分)一瓶质量为a千克的饮料中,如果含有b千克的糖,则我们就称分式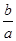 为这种饮料的“甜度”.同学们知道,橙汁饮料是用橙的果肉加工而成的,如果平均每个橙含糖a千克,可榨橙汁n千克.
为这种饮料的“甜度”.同学们知道,橙汁饮料是用橙的果肉加工而成的,如果平均每个橙含糖a千克,可榨橙汁n千克.
(1)用100个橙制成A种橙汁,用1000个橙制成B种橙汁,这两种橙汁的“甜度”有什么关系,为什么?
(2)若在(1)中的两种橙汁中都加入1千克的糖,加糖后的两种橙汁的甜度各是多少?哪一种更甜?
(8分)如图,小山的高AB=40m,B、D两点间水平距离为75m,在点D和山顶A处各建一个输电线铁塔,高度相等(即CD=AE),那么在两铁塔的顶端C、E之间架设一根高压线,这根高压线至少长多少米?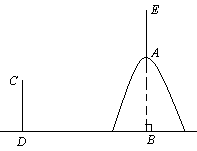
某工厂要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人的月工资分别为600元和1000元.
(1)设招聘甲种工种工人x人,工厂付给甲、乙两种工种的工人工资共y元,写出y(元)与x(人)的函数关系式
(2)现要求招聘的乙种工种的人数不少于甲种工种人数的2倍,问甲、乙两种工种
各招聘多少人时,可使得每月所付的工资最少?