(本题满分10分,第1小题5分,第2小题5分)等比数列{an}的前n项的和为Sn,已知S1,S3,S2成等差数列.
(1)求{an}的公比q;
(2)若a1-a3=3,求 .
.
已知在递增等差数列 中,
中, ,
, 成等比数列数列
成等比数列数列 的前n项和为Sn,且
的前n项和为Sn,且 .
.
(1)求数列 、
、 的通项公式;(2)设
的通项公式;(2)设 ,求数列
,求数列 的前
的前 和
和 .
.
在 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)若 ,求
,求 的值;(2)求sinA+sinC的最大值.
的值;(2)求sinA+sinC的最大值.
已知函数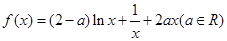
(1)当 时,求
时,求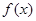 的极值
的极值
(2)当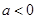 时,求
时,求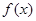 的单调区间
的单调区间
(3)若对任意的 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围。
的取值范围。
已知向量a=(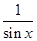 ,
, ),b=(2,cos2x).
),b=(2,cos2x).
(1)若x∈(0, ],试判断a与b能否平行?
],试判断a与b能否平行?
(2)若x∈(0, ],求函数f(x)=a·b的最小值.
],求函数f(x)=a·b的最小值.
在等差数列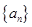 和等比数列
和等比数列 中,a1=2b1=2,b6=32,
中,a1=2b1=2,b6=32,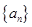 的前20项
的前20项
和S20=230.
(Ⅰ)求 和
和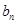 ;
;
(Ⅱ)现分别从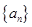 和
和 的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.
的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.