如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(﹣9,0),B(0,12),点C的坐标为(16,0),作射线CB,点D为射线CA上的一动点,过点D作DE⊥CB于点E,点P为直线AB上的一个动点,连结PD,PE,设CD长为t(t>0).
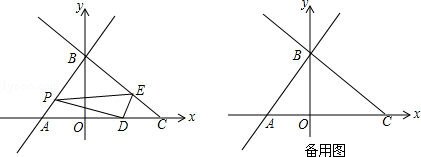
(1)当0<t<25时DE= ,BE= (均用含t的代数式表示);
(2)设△PDE的面积为S,请求出S关于t的函数关系式;
(3)当点D不在线段AO上时,在点D的其余运动过程中,若存在点D、P使得△PAD和△PBE相似,则求出所有满足条件的t的值.
解方程: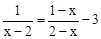 .
.
如图,矩形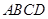 的对角线
的对角线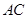 和
和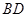 相交于点
相交于点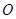 ,
,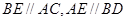 ,试判断四边形
,试判断四边形 的形状,并说明理由.
的形状,并说明理由.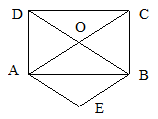
在如图的方格纸中,每个小正方形的边长都为l,△ABC与△A1B1C1构成的图形是中心对称图形.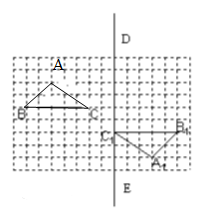
(1)画出此中心对称图形的对称中心O;
(2)画出将△A1B1C1,沿直线DE向上平移5格得到的△A2B2C2;
(3)要使△A2B2C2与△CC1C2重合,则△A2B2C2绕点C2顺时针方向旋转,至少要旋转多少度?(直接写出答案)
已知 ,
, ,求代数式
,求代数式 的值.
的值.
如果一元二次方程ax2+bx+c=0的两根x1、x2均为正数,且满足1< <2(其中x1>x2),那么称这个方程有“邻近根”.
<2(其中x1>x2),那么称这个方程有“邻近根”.
(1)判断方程 是否有“邻近根”,并说明理由;
是否有“邻近根”,并说明理由;
(2)已知关于x的一元二次方程mx2-(m-1)x-1=0有“邻近根”,求m的取值范围.