在如图的方格纸中，每个小正方形的边长都为l，△ABC与△A1B1C1构成的图形是中心对称图形．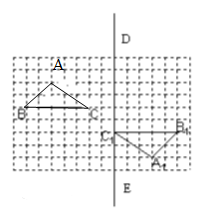
（1）画出此中心对称图形的对称中心O；
（2）画出将△A1B1C1，沿直线DE向上平移5格得到的△A2B2C2；
（3）要使△A2B2C2与△CC1C2重合，则△A2B2C2绕点C2顺时针方向旋转，至少要旋转多少度？（直接写出答案）
学校准备添置一批计算机．
方案1：到商家直接购买，每台需要7000元；
方案2：学校买零部件组装，每台需要6000元，另外需要支付安装工工资等其它费用合计3000元．设学校需要计算机x台，方案1与方案2的费用分别为y1、y2元．
（1）分别写出y1、y2的函数解析式；
（2）当学校添置多少台计算机时，两种方案的费用相同？
（3）若学校需要添置计算机50台，那么采用哪一种方案较省钱？说说你的理由
如图：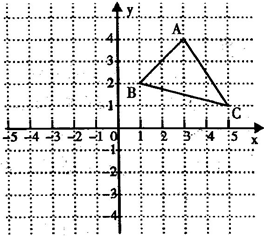
①写出A、B、C三点的坐标．A （） B（） C（）
②若△ABC各顶点的横坐标不变，纵坐标都乘以-1，请你在同一坐标系中描出对应的点 A′、B′、C′，并依次连接这三个点，所得的△A′B′C′与原△ABC有怎样的位置关系？
③在②的基础上，纵坐标都不变，横坐标都乘以-1在同一坐标系中描出对应的点A″、B″、C″，并依次连接这三个点，所得的△A″B″C″与原△ABC有怎样的位置关系？
已知一次函数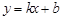
的图象如图所示．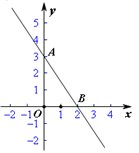
（1）求该一次函数的解析式；
（2）直接写出：当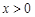
时，
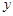的取值范围
如图，在四边形ABCD中，∠ABC=90°，AB＝3，BC＝4，DC＝12，AD=13，求四边形ABCD的面积．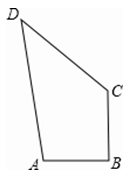
如图，二次函数的图象与x轴相交于点A（－3，0）、B（－1，0），与y轴相交于点C（0，3），点P是该图象上的动点；一次函数y＝kx－4k （k≠0）的图象过点P交x轴于点Q．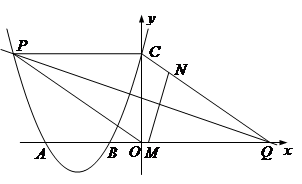
（1）求该二次函数的解析式；
（2）当点P的坐标为（－4，m）时，求证：∠OPC＝∠AQC；
（3）点M、N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M、N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．
①连接AN，当△AMN的面积最大时，求t的值；
②直线PQ能否垂直平分线段MN？若能，请求出此时点P的坐标；若不能，请说明你的理由．