学校准备添置一批计算机.
方案1:到商家直接购买,每台需要7000元;
方案2:学校买零部件组装,每台需要6000元,另外需要支付安装工工资等其它费用合计3000元.设学校需要计算机x台,方案1与方案2的费用分别为y1、y2元.
(1)分别写出y1、y2的函数解析式;
(2)当学校添置多少台计算机时,两种方案的费用相同?
(3)若学校需要添置计算机50台,那么采用哪一种方案较省钱?说说你的理由
如图,在平面直角坐标系xOy中,一次函数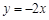 的图象与反比例函数
的图象与反比例函数 的图象的一个交点为A(-1,n).(1)求反比例函数
的图象的一个交点为A(-1,n).(1)求反比例函数 的解析式;(2)若P是坐标轴上一点,且PA=OA,试写出点
的解析式;(2)若P是坐标轴上一点,且PA=OA,试写出点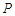 的坐标.
的坐标.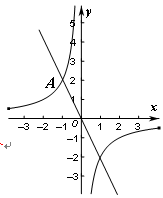
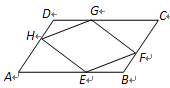
已知:如图,在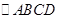 中,E、F、G、H分别是AB、BC、CD、DA上的点,且AE=CG,BF=DH.求证:
中,E、F、G、H分别是AB、BC、CD、DA上的点,且AE=CG,BF=DH.求证: ≌
≌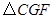 .
.
先化简,再求值: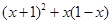 ,其中
,其中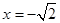 .
.
已知:如图,在平面直角坐标系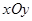 中,矩形OABC的边OA在
中,矩形OABC的边OA在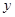 轴的正半轴上,OC在
轴的正半轴上,OC在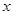 轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。
轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。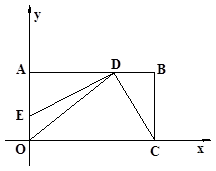
(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与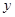 轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为
轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为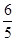 ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由。
两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC 不动,将△DEF进行如下操作: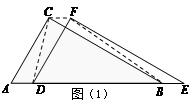
(1)如图(1),△DEF沿线段AB向右平移(即D点在线段AB上移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,它的面积是否变化,如果不变请求出其面积.如果变化,说明理由.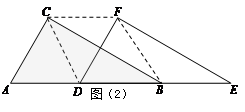
(2)如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.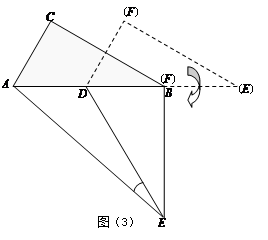
(3)如图(3),△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出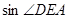 的值.
的值.