(本小题满分12分)某班级共有60名学生,先用抽签法抽取10名学生调查他们的学习情况。若抽查结果如下:
| 每周学习时间(小时) |
 |
 |
 |
 |
| 人数 |
2 |
4 |
3 |
1 |
完成频率分布直方图;
根据频率分布直方图估计该班学生每周学习的平均数、众数、中位数;
(3)若再从抽得的10中抽取3人,在抽取的3人中恰有一个来自第一组( 段)的条件下,求第二组至少抽取一人的概率.
段)的条件下,求第二组至少抽取一人的概率.
在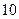 件产品中,有
件产品中,有 件一等品,
件一等品,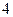 件二等品,
件二等品, 件三等品,从这
件三等品,从这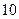 件产品中任取
件产品中任取 件
件
求:(1)取出的 件产品中一等品的件数
件产品中一等品的件数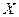 的分布列和数学期望
的分布列和数学期望
(2)取出的 件产品中一等品的件数多余二等品件数的概率
件产品中一等品的件数多余二等品件数的概率
在直角坐标系 中,以
中,以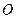 极点,
极点,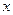 轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为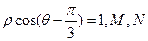 分别为
分别为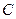 与
与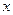 轴,
轴,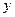 轴的交点
轴的交点
(1)写出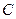 的直角坐标方程,并求出
的直角坐标方程,并求出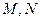 的极坐标
的极坐标
(2)设 的中点为
的中点为 ,求直线
,求直线 的极坐标方程
的极坐标方程
已知函数
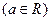 在
在 处,取得极值
处,取得极值
(1) 求实数 的值 (2) 求函数
的值 (2) 求函数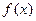 的单调区间,并指出其单调性。
的单调区间,并指出其单调性。
已知实数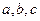 ,函数
,函数 当
当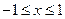 时,
时,
(1)证明: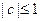 (2)证明:当
(2)证明:当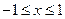 时,
时, ;
;
(3)设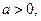 当
当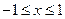 时,
时,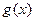 的最大值为2,求
的最大值为2,求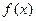
证明下列不等式:
(1) 都是正数,且
都是正数,且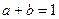 ,求证:
,求证: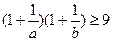 ;
;
(2)设实数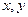 满足
满足 ,且
,且 ,求证:
,求证: