(本小题满分13分)受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关,某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年,现从该厂已售出的两种品牌轿车中随机抽取50辆,统计数据如下:
| 品牌 |
甲 |
乙 |
|||
首次出现故障时间 年 年 |
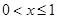 |
 |
 |
 |
 |
| 轿车数量(辆) |
2 |
3 |
45 |
5 |
45 |
| 每辆利润(万元) |
1 |
2 |
3 |
 |
 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求首次出现故障发生在保修期内的概率;
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为 ,生产一辆乙品牌轿车的利润为
,生产一辆乙品牌轿车的利润为 ,分别求
,分别求 的分布列;
的分布列;
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌轿车,若从生产一辆品牌轿车的利润均值的角度考虑,你认为应该生产哪种品牌的轿车?说明理由.
(本小题满分12分)已知向量 设函数
设函数
(1)求 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在 中
中 、
、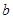 、
、 分别是角
分别是角 的对边,若
的对边,若
 的面积为
的面积为 ,求
,求 的值.
的值.
(本小题满分12分)在等差数列 中,
中, ,前
,前 项和为
项和为 ,等比数列
,等比数列 各项均为正数,
各项均为正数, ,且
,且 ,
, 的公比
的公比 .
.
(1)求 与
与 ;(2)求
;(2)求 .
.
平行六面体ABCD—A1B1C1D1中,AB=4,AD=3,AA1=5,∠BAD=90º ,
∠BAA1=∠DAA1=60º ,求AC1的长。
某抛物线形拱桥跨度是20米,拱高4米,在建桥时每隔4米需用一支柱支撑,求其中最长的支柱的长. 
已知椭圆C的焦点F1(-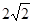 ,0)和F2(
,0)和F2(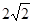 ,0),长轴长6。
,0),长轴长6。
(1)求椭圆C的标准方程。
(2)设直线 交椭圆C于A、B两点,求线段AB的中点坐标。
交椭圆C于A、B两点,求线段AB的中点坐标。