设函数 ,
,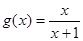 ,记
,记
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)求函数 在
在 上的最值.
上的最值.
(本题满分16分,第1小题4分,第2小题7分,第3小题5分)
如图,射线 所在的直线的方向向量分别为
所在的直线的方向向量分别为 ,
, ,点
,点 在
在 内,
内, 于
于 ,
, 于
于 ;
;
(1)若 ,
, ,求
,求 的值;
的值;
(2)若 ,
, 的面积为
的面积为 ,求
,求 的值;
的值;
(3)已知 为常数,
为常数, 的中点为
的中点为 ,且
,且 ,当
,当 变化时,求动点
变化时,求动点 轨迹方程;
轨迹方程;
(本题满分14分,第1小题6分,第2小题8分)
已知函数 的反函数为
的反函数为
(1)若 ,求实数
,求实数 的值;
的值;
(2)若关于 的方程
的方程 在区间
在区间 内有解,求实数
内有解,求实数 的取值范围;
的取值范围;
(本题满分14分,第1小题6分,第2小题8分)
在正方体 中,
中, 是棱
是棱 的中点.
的中点.
(1)求直线 与平面
与平面 所成角的大小(结果用反三角函数表示)
所成角的大小(结果用反三角函数表示)
(2)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,若存在,指明点
,若存在,指明点 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
已知函数 ,
, .
.
(1)若直线 是函数
是函数 的图像的一条对称轴,求
的图像的一条对称轴,求 的值;
的值;
(2)若 ,求
,求 的值域.
的值域.
已知函数 (
( ).
).
(Ⅰ)当 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,记函数
时,记函数 ,试求
,试求 的单调递减区间;
的单调递减区间;
(Ⅲ)设函数 (其中
(其中 为常数),若函数
为常数),若函数 在区间
在区间 上不存在极值,求
上不存在极值,求 的最大值.
的最大值.