(本小题满分12分)“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(Ⅰ)若某被邀请者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(Ⅱ)假定(Ⅰ)中被邀请到的3个人中恰有两人接受挑战.根据活动规定,现记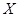 为接下来被邀请到的6个人中接受挑战的人数,求
为接下来被邀请到的6个人中接受挑战的人数,求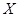 的分布列和均值(数学期望).
的分布列和均值(数学期望).
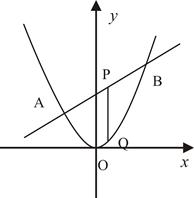
已知抛物线C: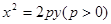 的焦点为F,直线
的焦点为F,直线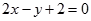 交抛物线
交抛物线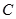 于
于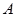 、
、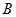 两点,
两点,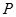 是线段
是线段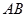 的中点,过
的中点,过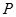 作
作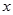 轴的垂线交抛物线
轴的垂线交抛物线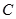 于点
于点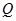 .
.
(1)若直线AB过焦点F,求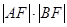 的值;
的值;
(2)是否存在实数 ,使
,使 是以
是以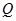 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图,在三棱锥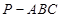 中,
中,
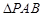 和
和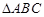 都是以
都是以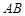 为斜边的等腰直角三角形,若
为斜边的等腰直角三角形,若 ,
,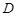 是
是 的中点
的中点
(1)证明: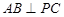 ;
;
(2)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知数列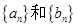 满足
满足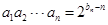 ,若
,若 为等比数列,且
为等比数列,且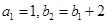 .
.
(1)求 ;
;
(2)设 ,求数列
,求数列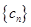 的前
的前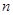 项和
项和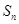 .
.
在△ABC中,角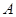 ,
, ,
,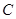 所对的边分别为
所对的边分别为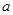 ,
, ,
, ,
,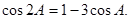 .
.
(1)求角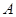 ;
;
(2)若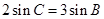 ,
,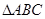 的面积
的面积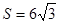 ,求
,求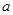 .
.
各项为正的数列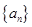 满足
满足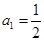 ,
,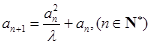 ,
,
(1)取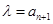 ,求证:数列
,求证:数列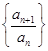 是等比数列,并求其公比;
是等比数列,并求其公比;
(2)取 时,令
时,令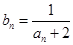 ,记数列
,记数列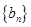 的前
的前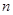 项和为
项和为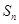 ,数列
,数列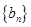 的前
的前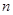 项之积为
项之积为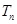 ,求证:对任意正整数
,求证:对任意正整数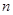 ,
,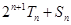 为定值.
为定值.