(本小题满分14分)已知函数 ,其中
,其中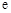 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若对任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)试探究当 时,方程
时,方程 解的个数,并说明理由.
解的个数,并说明理由.
设数列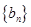 的前n项和为
的前n项和为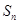 ,且
,且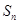 =2
=2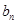 -2;数列
-2;数列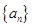 为等差数列,且
为等差数列,且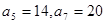 .
.
(1)求数列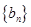 的通项公式;
的通项公式;
(2)求数列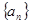 的前n项和
的前n项和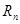 ;
;
(3)若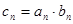 ,
, 为数列
为数列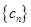 的前n项和,求
的前n项和,求
(本小题满分12分)已知关于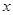 的不等式
的不等式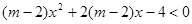 的解集为R,求实数
的解集为R,求实数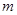 的取值范围.
的取值范围.
(本小题满分12分)某公司利用A、B两种原料生产甲、乙两种产品,每生产1吨产品所需要的原料及利润如下表所示:
| A种原料(单位:吨) |
B种原料(单位:吨) |
利润(单位:万元) |
|
| 甲种产品 |
1 |
2 |
3 |
| 乙种产品 |
2 |
1 |
4 |
公司在生产这两种产品的计划中,要求每种产品每天消耗A、B原料都不超过12吨.求每天生产甲、乙两种产品各多少吨,使公司获得总利润最大?最大利润是多少?
(本小题满分12分)已知△ABC的内角A,B,C所对的边分别为a,b,c且a=2,cosB= .
.
(1)求sinB的值;
(2)若b=4,求sinA的值;
(3)若△ABC的面积S△ABC=4,求b,c的值
(本小题满分10分)已知一元二次不等式 的解集为
的解集为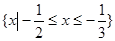 ,求不等式
,求不等式 的解集.
的解集.