若m是一个给定的正整数，如果两个整数a、b用m除所得的余数相同，则称a与b对m校同余，记作a≡b[mod（m）]，例如1≡13[mod（4）]，若22012≡r[mod（7）]，则r可能为（）
| A．5 | B．4 | C．3 | D．2 |
用秦九韶算法计算f（x）=3x3+2x2+4x+6，要用到乘法和加法的次数分别为（）
| A．3次，3次 | B．4次，4次 | C．4次，3次 | D．3次，4次 |
下列各数中最小的一个是（）
| A．111111（2） | B．210（6） | C．1000（4） | D．81（9） |
设a，b，m为正整数，若a和b除以m的余数相同，则称a和b对m同余． 记作a=b（modm），已知a=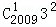
+
+…+
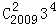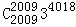，b=a（mod10），则b的值可以是（）
| A．1012 | B．2009 | C．3003 | D．6001 |
已知m是一个给定的正整数，如果两个整数a，b被m除得的余数相同，则称a与b对模m同余，记作a≡b（modm），例如：5≡13（mod4）．若22010≡r（mod7），则r可以为（）
| A．2008 | B．2009 | C．2010 | D．2011 |
的方程
在区间[k-1,k+1]上有两个不相等的实根，则实数
的取值范围是（ ）
