(本小题满分12分)如图所示,在平面直角坐标系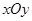 中,设椭圆
中,设椭圆 ,其中
,其中 ,过椭圆
,过椭圆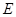 内一点
内一点
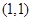 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 和
和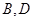 ,且满足
,且满足 ,
, ,其中
,其中 为正常数. 当点
为正常数. 当点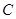 恰为椭圆的右顶点时,对应的
恰为椭圆的右顶点时,对应的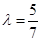 .
.
(1)求椭圆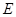 的离心率;
的离心率;
(2)求 与
与 的值;
的值;
(3)当 变化时,
变化时,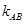 是否为定值?若是,请求出此定值;若不是,请说明理由.
是否为定值?若是,请求出此定值;若不是,请说明理由.
在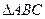 中,
中,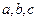 分别为内角
分别为内角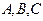 所对的边,且满足
所对的边,且满足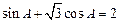 .
.
(Ⅰ)求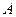 的大小;
的大小;
(Ⅱ)现给出三个条件:①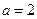 ; ②
; ②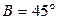 ;③
;③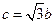 .
.
试从中选出两个可以确定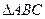 的条件,写出你的选择并以此为依据求
的条件,写出你的选择并以此为依据求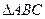 的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)
的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)
(本小题满分13分)
给出定义在(0,+∞)上的三个函数: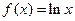 ,
,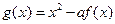 ,
,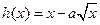 ,已知
,已知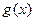 在x=1处取极值.
在x=1处取极值.
(Ⅰ)确定函数h(x)的单调性;
(Ⅱ)求证:当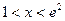 时,恒有
时,恒有 成立;
成立;
(Ⅲ)把函数h(x)的图象向上平移6个单位得到函数h1(x)的图象,试确定函数y=g(x)-h1(x)的零点个数,并说明理由.
(本小题满分13分)
过圆 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P关于点D(9,0)的对称点为E,O为坐标原点,将线段OP绕原点O依逆时针方向旋转90°后,所得线段为OF,求|EF|的取值范围.
(本小题满分13分)
某县为了贯彻落实党中央国务院关于农村医疗保险(简称“医保”)政策,制定了如下实施方案:2009年底通过农民个人投保和政府财政投入,共集资1000万元作为全县农村医保基金,从2010年起,每年报销农民的医保费都为上一年底医保基金余额的10%,并且每年底县财政再向医保基金注资m万元(m为正常数).
(Ⅰ)以2009年为第一年,求第n年底该县农村医保基金有多少万元?
(Ⅱ)根据该县农村人口数量和财政状况,县政府决定每年年底的医保基金要逐年增加,同时不超过1500万元,求每年新增医保基金m(单位:万元)应控制在什么范围内.
(本小题满分12分)
如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.
(Ⅰ)求二面角M-AC-B大小的正切值;
(Ⅱ)求三棱锥P-MAC的体积.
 |