( 本小题满分12分)
已知直线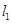 :
: 与
与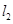 :
: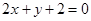 的交点为
的交点为 .
.
(1)求交点 的坐标;
的坐标;
(2)求过点 且平行于直线
且平行于直线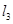 :
: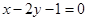 的直线方程;
的直线方程;
(3)求过点 且垂直于直线
且垂直于直线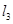 :
: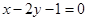 直线方程.
直线方程.
在△ 中,角
中,角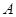 、
、 、
、 的对边分别为
的对边分别为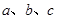 ,若
,若 ,
,
且 .(1)求
.(1)求 的值;(2)若
的值;(2)若 ,求△
,求△ 的面积.
的面积.
(本小题满分12分)
(Ⅰ)求以下不等式的解集:
(1) 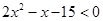 (2)
(2) 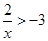
(Ⅱ)若关于x的不等式 的解集为
的解集为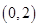 ,求实数m的值.
,求实数m的值.
(本小题满分14分)已知数列{an}的前n项和为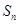 ,且满足
,且满足 ,数列
,数列 满足
满足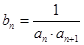 ,
,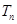 为数列
为数列 的前n项和.
的前n项和.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若对任意的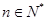 ,不等式
,不等式 恒成立,求实数
恒成立,求实数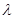 的取值范围;
的取值范围;
(Ⅲ)是否存在正整数m,n(1<m<n),使得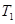 ,
, ,
,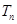 成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
(本小题满分14分)
已知点 到直线l:
到直线l: 的距离为
的距离为 .数列{an}的首项
.数列{an}的首项 ,且点列
,且点列 均在直线l上.
均在直线l上.
(Ⅰ)求b的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)求数列 的前n项和
的前n项和 .
.
(本小题满分14分)如图所示,某海岛上一观察哨A在上午11时测得一轮船在海岛北偏东 的C处,12时20分测得船在海岛北偏西
的C处,12时20分测得船在海岛北偏西 的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?
的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?