(本小题满分14分)
已知点 到直线l:
到直线l: 的距离为
的距离为 .数列{an}的首项
.数列{an}的首项 ,且点列
,且点列 均在直线l上.
均在直线l上.
(Ⅰ)求b的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)求数列 的前n项和
的前n项和 .
.
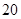 名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
(1)求频率分布直方图中 的值;
的值;
(2)分别求出成绩落在 与
与 中的学生人数;
中的学生人数;
(3)从成绩在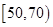 的学生中任选
的学生中任选 人,求此
人,求此 人的成绩都在
人的成绩都在 中的概率.
中的概率.
如图,在四棱锥 中,底面
中,底面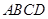 是
是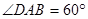 且边长为
且边长为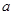 的菱形,侧面
的菱形,侧面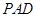 是等边三角形,且平面
是等边三角形,且平面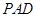 ⊥底面
⊥底面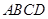 ,
,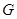 为
为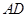 的中点.
的中点.
(1)求证: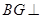 平面
平面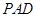 ;
;
(2)求 点G到平面PAB的距离。
(本小题满分12分)已知数列 的通项公式为
的通项公式为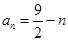 ,
,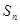 是
是 的前
的前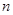 项的和。
项的和。
(1)证明:数列 是等差数列
是等差数列
(2)求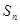 的最大值以及相应的
的最大值以及相应的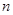 的值。
的值。
(本小题满分10分)选修4-5:不等式选讲
已知函数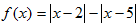
(1)若关于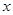 的不等式
的不等式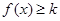 有解,求
有解,求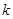 的最大值;
的最大值;
(2)求不等式: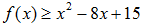 的解集.
的解集.
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线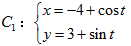 (
(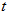 为参数),
为参数),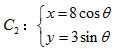 (
(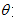 为参数).
为参数).
(1)化 的方程为普通方程;
的方程为普通方程;
(2)若 上的点对应的参数为
上的点对应的参数为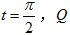 为
为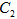 上的动点,求
上的动点,求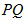 中点
中点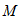 到直线
到直线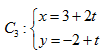 (
(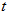 为参数)距离的最小值.
为参数)距离的最小值.