如图所示，充电后的平行板电容器水平放置，电容为C，极板间距离为d，上极板正中有一小孔．质量为m，电荷量为＋q的小球从小孔正上方高h处由静止开始下落，穿过小孔到达下极板处速度恰为零(空气阻力忽略不计，极板间电场可视为匀强电场，重力加速度为g)．求：
(1)小球到达小孔处的速度；
(2)两极板间的电势差的大小；
(3)电容器所带电荷量.
半径为R的圆柱体放在水平地面上，在距地面(3+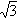
)R的上方放置一个与地面平等的平面镜MN，在圆柱体左侧的地上有一点光源S，圆
柱体右侧AB部分没有光线照射到.其截面图如图所示.已知：
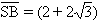R。求AB的宽度.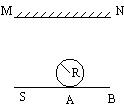
半径为R的半圆柱形玻璃砖，横截面如图所示。O为圆心。已知玻璃的折射率为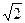
。当光由玻璃射向空气时，发生全反射的临界角为45°，一束与MN平面成45°的平行光束射到玻璃砖的半圆柱面上，经玻璃折
射后，有部分光能从MN平面上射出。求能从MN平面射出的光束的宽度为多少？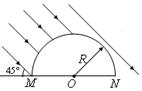
如图所示，一小球A与一个白炽灯泡S紧靠在一起，小球在灯泡的右侧，小球可看做质点，灯泡可视为一点光源，P为一个竖直放置的屏幕，P与
光源之间的距离为L，今将小球以水平速V0向右抛出。
（1）试证明小球运动过程中(没有碰到屏幕)它在屏幕上的影子将沿屏幕向下做匀速运动。
（2）求影的运动速度。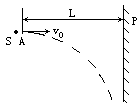
如图所示，一个边长L="10" cm，匝数
N=100匝的正方形线圈abcd在匀强磁场中绕垂直于磁感线的对称轴
匀速转动，磁感应强度B=0．50 T，角速度
，外电路电阻R=4．0Ω，
线圈内阻r=1.0Ω。求：
（1）线圈转动的周期和感应电动势的最大值；
（2）写出线圈由图中所示位置开始计时时，感应电动势的瞬时表达式；
（3）交流电压表的示数；
（4）2 mm内，电阻霞上的发热量。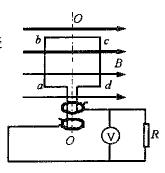
如图所示。一块涂有碳黑的玻璃板，质量为2kg，在拉力F="24" N的作用下
，由静止开始竖直向上做匀加速运动．一个装有水平振针的振动的固定电动音叉在玻璃板上画出了图示曲线，量得OA=1cm，OB=4cm，OC=9cm。求电动音叉的振动频率的大小。（g=10m/s2）