如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.
如图,在平面直角坐标系中,A(1, 2),B(3, 1),C(-2, -1).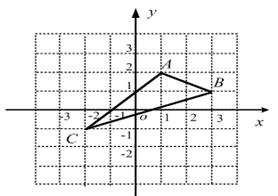
(1)在图中作出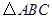 关于
关于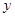 轴对称的
轴对称的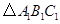 .
.
(2)写出点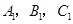 的坐标.A1 _________ B1________ C1 ________.
的坐标.A1 _________ B1________ C1 ________.
如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,直线BD与直线CE相交于点O.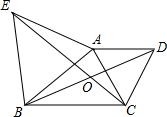
(1)求证:CE=BD;
(2)如果当点A在直线BC的上方变化位置,且保持∠ABC和∠ACB都是锐角,那么∠BOC的度数是否会发生变化?若变化,请说明理由;若不变化,请求出∠BOC的度数:
(3)如果当点A在直线BC的上方变化位置,且保持∠ACB是锐角,那么∠BOC的度数是否会发生变化?若变化,请直接写出变化的结论,不需说明理由;若不变化,请直接写明结论.
如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)求证:BH=AC;
(2)求证:BG2-GE2=EA2.
师在一次“探究性学习”课中,给出如下数表: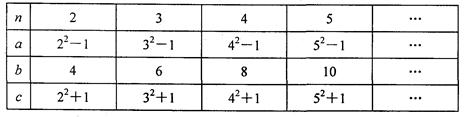
(1)请你分别认真观察线段a、b、c的长与n之间的关系,用含n(n为自然数,且n>1)的代数式表示:
a=,b=,c=.
(2)猜想:以线段a、b、c为边的三角形是否是直角三角形?并说明你的理由.