如图是某风景区的旅游路线示意图,其中B、C、D为风景点,E为两条路的交叉点,图中的数据为相应两点间的路程(单位:km),小新从A处出发,以2km/h的速度步行游览,每个景点的逗留时
间均为0.5小时.
(1)当他沿着路线A—D—C—E—A游览回到A处时,共用了3小时,求C—E的路程;
(2)若小新打算从A处出发,步行速度与在每个景点逗留的时间不变,且在4小时内看完三个景点返回到A处,请你为他设计一条步行路线,并说明你的设计理由(不考虑其他因素)( 4分)
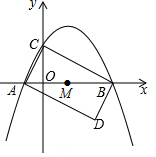
如图,抛物线 y= ax 2+ bx+2与 x轴相交于 A(﹣1,0), B(4,0)两点,与 y轴相交于点 C.
(1)求抛物线的解析式;
(2)将△ ABC绕 AB中点 M旋转180°,得到△ BAD.
①求点 D的坐标;
②判断四边形 ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点 P,使△ BMP与△ BAD相似?若存在,请求出所有满足条件的 P点的坐标;若不存在,请说明理由.
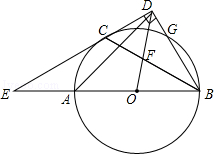
如图, AB为⊙ O的直径, C, G是⊙ O上两点,过点 C的直线 CD⊥ BG于点 D,交 BA的延长线于点 E,连接 BC,交 OD于点 F,且 BC平分∠ ABD.
(1)求证: CD是⊙ O的切线;
(2)若 ,求∠ E的度数;
(3)连结 AD,在(2)的条件下,若 CD=2 ,求 AD的长.
如图,直线 y=﹣ x+2与反比例函数 y= ( k≠0)的图象交于 A( a,3), B(3, b)两点,过点 A作 AC⊥ x轴于点 C,过点 B作 BD⊥ x轴于点 D.
(1)求 a, b的值及反比例函数的解析式;
(2)若点 P在直线 y=﹣ x+2上,且 S △ ACP= S △ BDP,请求出此时点 P的坐标;
(3)在 x轴正半轴上是否存在点 M,使得△ MAB为等腰三角形?若存在,请直接写出 M点的坐标;若不存在,说明理由.

如图,在平行四边形 ABCD中, E, F分别是 AB, BC边上的中点, CE⊥ AB,垂足为 E, AF⊥ BC,垂足为 F, AF与 CE相交于点 G;
(1)求证:△ CFG≌△ AEG;
(2)若 AB=6,求四边形 AGCD的对角线 GD的长.

小美周末来到公园,发现在公园一角有一种"守株待兔"游戏.游戏设计者提供了一只兔子和一个有 A, B, C, D, E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从 A, B两个出入口放入:②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值4元的小兔玩具,否则应付费3元.
(1)请用画树状图的方法,列举出该游戏的所有可能情况;
(2)小美得到小兔玩具的机会有多大?
(3)假设有125人次玩此游戏,估计游戏设计者可赚多少元.