一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后都停留一段时间，然后分别按原速一同驶往甲地后停车．设慢车行驶的时间为x小时，两车之间的距离为y千米，图中折线表示y与x之间的函数图象，请根据图象解决下列问题：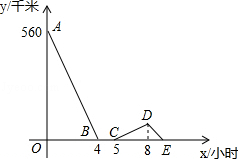
（1）甲乙两地之间的距离为 千米；
（2）求快车和慢车的速度；
（3）求线段DE所表示的y与x之间的函数关系式，并写出自变量x的取值范围．
下图是输水管的切面，阴影部分是有水部分，其中水面AB宽16㎝，水最深4㎝，
（1）求输水管的半径。
（2）当∠AOB＝120°时，求阴影部分的面积.
一透明的口袋中装有3个球,这3个球分别标有1,2,3,这些球除了数字外都相同.
（1）如果从袋子中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?
（2）小明和小亮玩摸球游戏,游戏的规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小亮随机摸出一个球,记下数字.谁摸出的球的数字大,谁获胜.请你用树状图或列表法分析游戏规则对双方是否公平?并说明理由.
已知
是关于x的一元二次方程
的两个实数根，且
，
求：（1）k的值；
（2）
的值.
如图，△ABC三个顶点的坐标分别为A（-3，-1）、B（-4，-3）C（-2，-5）：
（1）在图中作出△ABC关于y轴对称的图形△A1B1C1；并写出A1、B1、C1点的坐标。
（2）在图中作出△ABC关于原点对称的图形△A2B2C2；并写出A2、B2、C2点的坐标.
先化简,再求值:（x-1）÷
,其中x为方程x2+3x+2=0的根.