如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)C(-2,-5):
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1;并写出A1、B1、C1点的坐标。
(2)在图中作出△ABC关于原点对称的图形△A2B2C2;并写出A2、B2、C2点的坐标.
为了响应某市人民政府“形象重于生命”的号召,在甲建筑物上从点A到点E挂一长为30米的宣传条幅.如图所示,在乙建筑物的顶点D处测得条幅顶端点A的仰角为45°,测得条幅底端点E的俯角为30°,求底部不能直接到达的甲、乙两建筑物之间的水平距离BC.(精确到1米)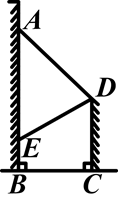
某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.如图,当飞机到达距离海面3000米的高空C处时,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°.请问:此时渔政船和渔船相距多远?(结果保留根号)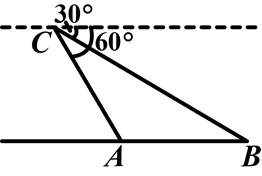
如图,山上有一座铁塔,山脚下有一矩形建筑物ABCD,且建筑物周围没有开阔平整地带.该建筑物顶端宽度AD和高度DC都可直接测得,从A、D、C三点可看到塔顶端H.可供使用的测量工具有皮尺、测角仪.
(1)请你根据现有条件,充分利用矩形建筑物,设计一个测量塔顶端到地面高度HG的方案.具体要求如下:①测量数据尽可能少;②在所给图形上,画出你设计的测量平面图,并将应测数据标记在图形上(如果测A、D间距离,用m表示;如果测D、C间距离,用n表示;如果测角,用α、β、γ表示);
(2)根据你测量的数据,计算塔顶端到地面的高度HG(用字母表示,测角仪高度忽略不计).
(贵州六盘水)为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动.下图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得数据如下:
①小明的身高DC=1.5m;
②小明的影长CE=1.7m;
③小明的脚到旗杆底部的距离BC=9m;
④旗杆的影长BF=7.6m;
⑤从D点看A点的仰角为30°.
请选择你需要的数据,求出旗杆的高度.(计算结果精确到0.1,参考数据: ,
, )
)
某校九(1)班的同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
(1)如图①,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求α的度数.
(2)如图②,第二小组用皮尺量得EF的长为16米(E为护墙上的端点),EF的中点距离地面FB的高度为1.9米,请你求出E点距离地面FB的高度.
(3)如图③,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P处测得旗杆顶端A的仰角为45°,向前走4米到达点Q处,测得A的仰角为60°,求旗杆的高度AE(精确到0.1米.参考数据:tan60°≈1.732,tan30°≈0.577, ,
, ).
).