如图,山上有一座铁塔,山脚下有一矩形建筑物ABCD,且建筑物周围没有开阔平整地带.该建筑物顶端宽度AD和高度DC都可直接测得,从A、D、C三点可看到塔顶端H.可供使用的测量工具有皮尺、测角仪.
(1)请你根据现有条件,充分利用矩形建筑物,设计一个测量塔顶端到地面高度HG的方案.具体要求如下:①测量数据尽可能少;②在所给图形上,画出你设计的测量平面图,并将应测数据标记在图形上(如果测A、D间距离,用m表示;如果测D、C间距离,用n表示;如果测角,用α、β、γ表示);
(2)根据你测量的数据,计算塔顶端到地面的高度HG(用字母表示,测角仪高度忽略不计).
求下列各式中x的值:(1)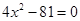 ;(2)
;(2)
如图,点O在直线AD上,∠EOC=90°,∠DOB=90°
(1)若∠EOD=50°, 
①求∠AOC的度数;
②若OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)将∠EOC绕O点旋转一圈,设∠EOD为α(0°<α<180°) 当α为何值时,直线OC平分∠BOD.
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体。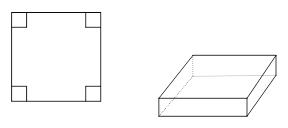
(1)如果剪去的小正方形的边长为xcm,请用x来表示这个无盖长方体的容积;
(2)当剪去的小正方体的边长x的值分别为3cm和3.5cm时,比较折成的无盖长方体的容积的大小。
已知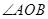 是一个直角,在角的内部作射线
是一个直角,在角的内部作射线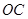 ,再分别作
,再分别作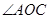 和
和 的平分线
的平分线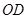 、
、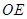 .
.
(1)如图①,当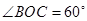 时,则求
时,则求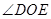 的度数;
的度数;
(2)如图②,当射线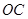 在
在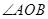 内绕
内绕 点旋转时,
点旋转时,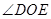 的大小是否发生变化?若变化,说明理由;若不变,求
的大小是否发生变化?若变化,说明理由;若不变,求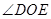 的度数.
的度数.
“老牛:累死我了!
小马:你还累?这么大的个,才比我多驮了2个。
老牛:哼,我从你背上拿来1个,我的包裹数就是你的2倍!
小马:真的?!”
根据老牛和小马的对话,你能求出它们各驮了多少个包裹吗?