(本题共14分)已知函数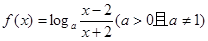 。
。
(1)求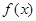 的定义域;
的定义域;
(2)判定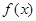 的奇偶性;
的奇偶性;
(3)是否存在实数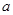 ,使得
,使得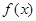 的定义域为
的定义域为 时,值域为
时,值域为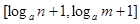 ?若存在,求出实数
?若存在,求出实数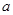 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
已知函数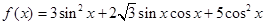 .
.
(1)若 ,求
,求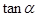 的值;
的值;
(2)设△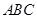 三内角
三内角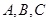 所对边分别为
所对边分别为 且
且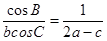 ,求
,求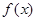 在
在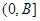 上的值域.
上的值域.
已知函数
(Ⅰ)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(Ⅱ)令g(x)= f(x)-x2,是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(Ⅲ)当x∈(0,e]时,证明: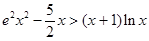
已知中心在原点O,焦点F1、F2在x轴上的椭圆E经过点C(2,2),且抛物线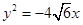 的焦点为F1.
的焦点为F1.
(Ⅰ)求椭圆E的方程;
(Ⅱ)垂直于OC的直线l与椭圆E交于A、B两点,当以AB为直径的圆P与y轴相切时,求直线l的方程和圆P的方程.
如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点,且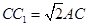 .
.
(Ⅰ)求证:CN∥平面AMB1;
(Ⅱ)求证: B1M⊥平面AMG.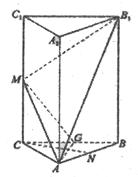
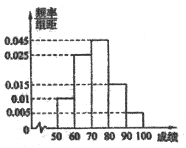
山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.