已知a与b互为相反数,m、n互为倒数,求a+1+mn+b的值.
如图所示,⊙I是△ABC的内切圆,AB=9,BC=8,CA=10,点D、E分别为AB、AC上的点,且DE是⊙I的切线,求△ADE的周长.
如图,已知扇形AOB的半径为12,OA⊥OB,C为OB上一点,以OA为直径的半圆O1与以BC为直径的半圆O2相切于点D.求图中阴影部分面积.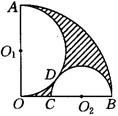
如图6,从点P向⊙O引两条切线PA,PB,切点为A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm,求AC的长.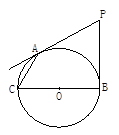
如图,抛物线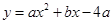 经过
经过 、
、 两点,与
两点,与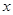 轴交于另一点
轴交于另一点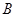 .
.求抛物线的解析式
已知点
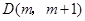 在第一象限的抛物线上,求点
在第一象限的抛物线上,求点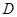 关于直线
关于直线 对称的点的坐标;
对称的点的坐标;在(2)的条件下,连接
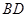 ,点
,点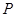 为抛物线上一点,且
为抛物线上一点,且 ,求点
,求点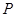 的坐标.
的坐标.
在复习《反比例函数》一课时,同桌的小明和小芳有一个问题观点不一致.小明认为如果两次分别从1~6六个整数中任取一个数,第一个数作为点 的横坐标,第二个数作为点
的横坐标,第二个数作为点 的纵坐标,则点
的纵坐标,则点 在反比例函数
在反比例函数 的图象上的概率一定大于在反比例函数
的图象上的概率一定大于在反比例函数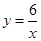 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?试用列表或画树状图的方法列举出所有点
 的情形;
的情形;分别求出点
 在两个反比例函数的图象上的概率,并说明谁的观点正确.
在两个反比例函数的图象上的概率,并说明谁的观点正确.