列方程解应用题:一件工作,甲单独完成要20小时,乙单独完成要12小时,现在两人合作,一段时间后,乙有事退出,结果甲又单独干了4小时才完成,两人合作了多长时间?
(本题满分7分.)如图7,反比例函数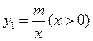 的图像与一次函数
的图像与一次函数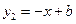 的图象交于点A、B,其中A(1,2).
的图象交于点A、B,其中A(1,2).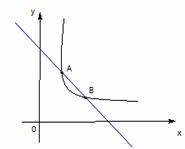
(1)求m,b的值;
(2)求点B的坐标,并写出 时,
时,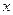 的取值范
的取值范 围.
围.
(本题满分7分)如图6,我市某展览厅东面有两个入口A、B,南面、西面、北面各有一个出口.小华任选择一个入口进入展览大厅,参观结束后任选一个出口离开.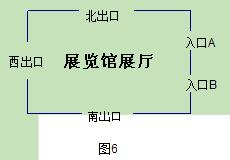
(1)利用树状图表示她从进入到离开的所有路径;
(2) 她从入口A进入展厅并从北出口离开的概率是多少?
(本题满分7分)如图5,点P在平行四边形ABCD的CD边上,连结BP并延长与AD的延长线交于点Q.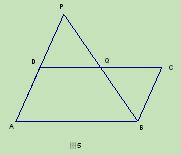
(1)求证:△DQP∽△CBP;
(2)当△DQP≌△CBP,且AB=8时,求DP的长.
如图,在平面直角坐标系中,点A(-4,4),点B(-4,0),将△ABO绕原点O按顺时针方向旋转135°得到△ 。回答下列问题:(直接写结果)
。回答下列问题:(直接写结果)
(1)∠AOB=  °;
°;
(2)顶点A从开始到 经过的路径长为
经过的路径长为 ;
;
(3)点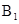 的坐标为
的坐标为
王老师对河东中学九(一)班的某次模拟考试成绩进行统计后,绘制了频数分布直方图(如图,分数取正整数,满分120分).根据图形,回答下列问题:(直接填写结果)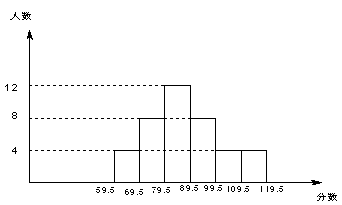
(1)该班有 名学生;
名学生;
(2)89.5 --99.5这一组的频数是 ,频率是
,频率是
(3)估算该班这次数学模拟考试的平均成绩是 .
.