某地举办乒乓球比赛的费用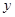 (元)包括两部分:一部分是租用比赛场地等固定不变的费用
(元)包括两部分:一部分是租用比赛场地等固定不变的费用 ,另一部分与参加比赛的人数
,另一部分与参加比赛的人数 (人)成正比例. 当
(人)成正比例. 当 时,
时,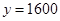 ,当
,当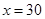 时,
时,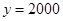 .
.
(1)求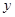 与
与 之间的函数关系式;
之间的函数关系式;
(2)如果有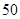 名运动员参加比赛,且全部费用由运动员分摊,那么每名运动员需要支付多少元?
名运动员参加比赛,且全部费用由运动员分摊,那么每名运动员需要支付多少元?
如果|3x+2|+|2y﹣1|=0,那么点P(x,y)和点Q(x+1,y﹣2)分别在哪个象限?
在同一直角坐标系中分别描出点A(﹣3,0)、B(2,0)、C(1,3),再用线段将这三点首尾顺次连接起来,求△ABC的面积与周长.
在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.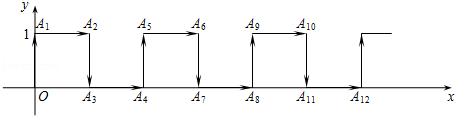
(1)填写下列各点的坐标:A4,A8;
(2)写出点A4n的坐标(n为正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
(1)解不等式组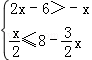 ,并把它的解集在数轴上表示出来;
,并把它的解集在数轴上表示出来;
(2)若(1)中的不等式组的所有整数解的和为a,试判断点P(6﹣a,2a﹣8)在哪个象限?
根据不等式的性质把下列不等式化成x>a或x<a的形式.
(1)x+7>9
(2)6x<5x﹣3
(3)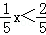 .
.