(1)解不等式组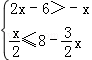 ,并把它的解集在数轴上表示出来;
,并把它的解集在数轴上表示出来;
(2)若(1)中的不等式组的所有整数解的和为a,试判断点P(6﹣a,2a﹣8)在哪个象限?
已知: ,
, .求代数式
.求代数式 的值.
的值.
解方程组
如图, 和
和 分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
(1)B出发时与A相距千米;
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是小时;
(3)B出发后小时与A相遇;
(4)若B的自行车不发生故障,保持出发时的速度前进,那么B几小时后与A相遇,相遇点离B的出发点多少千米?在图中标出这个相遇点C.
某一天,文具经营户花360元从文具批发市场批发了自动铅笔和钢笔共80支,到文具店去卖,自动铅笔和钢笔当天的批发价与零售价如下表所示:
| 品名 |
钢笔 |
自动铅笔 |
| 批发价(元/支) |
4.8 |
4 |
| 零售价(元/支) |
7.2 |
5.6 |
问:他卖完这些自动铅笔和钢笔可赚多少钱?
如图,点A、B在数轴上分别表示有理数 、
、 ,在数轴上A、B两点之间的距离
,在数轴上A、B两点之间的距离 .
.
回答下列问题:
(1)数轴上表示1和 的两点之间的距离是;(1分)
的两点之间的距离是;(1分)
(2)数轴上表示 和
和 的两点之间的距离表示为;(1分)
的两点之间的距离表示为;(1分)
(3)若 表示一个有理数,请你结合数轴求
表示一个有理数,请你结合数轴求 的最小值.(2分)
的最小值.(2分)