（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E． 证明：DE=BD+CE．
如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
（3）拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状． 
2013年4月20日8时，四川省芦山县发生7.0级地震，某市派出抢险救灾工程队赶芦山支援，工程队承担了2400米道路抢修任务，为了让救灾人员和物资尽快运抵灾区，实际施工速度比原计划每小时多修40米，结果提前2小时完成，求原计划每小时抢修道路多少米？
如图，C岛位于我南海A港口北偏东60方向，距A港口60
海里处，我海监船从A港口出发，自西向东航行至B处时，接上级命令赶赴C岛执行任务，此时C岛在B处北偏西45°方向上，海监船立刻改变航向以每小时60海里的速度沿BC行进，则从B处到达C岛需要多少小时？
先化简，再求值：
，其中x=﹣2．
解不等式组：
．
如图所示，在Rt△ABC中，AB=BC=4，∠ABC=90°，点P是△ABC的外角∠BCN的角平分线上一个动点，点P′是点P关于直线BC的对称点，连结PP′交BC于点M，BP′交AC于D，连结BP、AP′、CP′．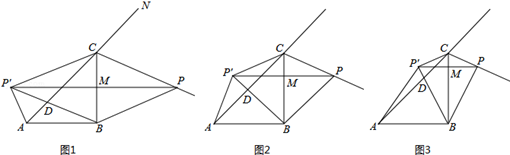
（1）若四边形BPCP′为菱形，求BM的长；
（2）若△BMP′∽△ABC，求BM的长；
（3）若△ABD为等腰三角形，求△ABD的面积．