如图，在平面直角坐标系xOy中，二次函数
的顶点为D（1，-1），且与x轴交于O，A两点，二次函数的图象记作
，把向右平移m（m>0）个单位得到的图象记作
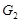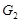，与x轴交于B，C两点，且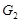与相交于点P．
（1）①求a，b的值；②求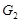的函数表达式（用含m的式子表示）；
（2）若△PBC的面积记作S，求S与m的关系式；（3）是否存在△PBC的面积是△DAB的面积的3倍，若存在，直接写出m的值；若不存在，说明理由．
伦敦奥运会将于2012年7月27日开幕，组委会备选的开幕式甲、乙两支仪仗队队员的身高（单位：厘米）如下：
甲队：178，177，179，178，177，178，177，179，178，179；
乙队：178，179，176，178，180，178，176，178，177，180；
（1）将下表填完整：
| 身高（厘米） |
176 |
177 |
178 |
179 |
180 |
| 甲队（人数） |
3 |
4 |
0 |
||
| 乙队（人数） |
2 |
1 |
1 |
（2）甲队队员身高的平均数为厘米，乙队队员身高的平均数为厘米；
（3）你认为哪支仪仗队更为整齐？简要说明理由．
平行四边形ABCD中，AB=5，AD＝8，∠C、∠D的平分线分别交 AD、BC与点E、F，且AF⊥BC．
（1）求tan∠ADF；
（2）求CE的长．
解方程：
计算：
已知：半圆
的半径
，
是
延长线上一点，过线段
的中点
作垂线交
于点
，射线
交于点
，联结
．
（1）若
，求弦
的长．
（2）若点在
上时，设
，
，求
与
的函数关系式及自变量的取值范围；
（3）设的中点为
，射线
与射线交于点
，当
时，请直接写出
的值．