某公司经销一种商品,每件商品的成本为50元,经市场的调查,在一段时间内,销售量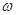 (件)随销售单价x(元/件)的变化而变化,具体关系式为
(件)随销售单价x(元/件)的变化而变化,具体关系式为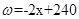 ,
,
设这种商品在这段时间内的销售利润为y(元),解答如下问题:
(1)求y与x的关系式;
(2)当x取何值时,y的值最大?
(3)如果物价部门规定这种商品的销售单价不得高于80元/件,公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
解方程:
(本题12分)如图,抛物线 经过
经过 的三个顶点,已知
的三个顶点,已知
 轴,点
轴,点 在
在 轴上,点
轴上,点 在
在 轴上,且
轴上,且 .
.
(1)求抛物线的对称轴;
(2)写出A,B,C三点的坐标(A,B,C三点的坐标只需写出答案),并求抛物线的解析式;
(3)探究:若点
 是抛物线对称轴上且在
是抛物线对称轴上且在 轴下方的动点,是否存在
轴下方的动点,是否存在 是等腰三角形.若存在,求出所有符合条件的点
是等腰三角形.若存在,求出所有符合条件的点 坐标;不存在,请说明理由.
坐标;不存在,请说明理由.
(本题12分)AB是⊙O的直径,点E是半圆上一动点(点E与点A、B都不重合),点C是BE延长线上的一点,且CD⊥AB,垂足为D,CD与AE交于点H,点H与点A不重合。
(1)求证:△AHD∽△CBD
(2)若CD=AB=2,求HD+HO的值。
(本题10分)如图所示,已知圆锥底面半径r=10cm,母线长为30cm.
(1)求它的侧面展开图的圆心角和表面积.
(2)若一蚂蚁从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.求证: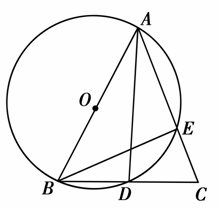
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)BC2=2AB·CE.