将 绕点
绕点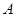 按逆时针方向旋转
按逆时针方向旋转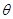 度,并使各边长变为原来的
度,并使各边长变为原来的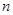 倍,得
倍,得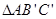 ,如图①,我们将这种变换记为
,如图①,我们将这种变换记为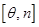 .
.
(1)如图①,对 作变换
作变换 得
得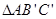 ,则
,则 ;直线
;直线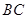 与直线
与直线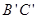 所夹的锐角为 度;
所夹的锐角为 度;
(2)如图②, 中,
中, ,
,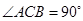 ,对
,对 作变换
作变换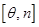 得
得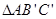 ,使点
,使点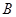 、
、 、
、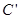 在同一直线上,且四边形
在同一直线上,且四边形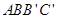 为矩形,求
为矩形,求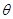 和
和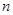 的值;
的值;
(3)如图③, 中,
中,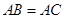 ,
, ,
,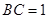 ,对
,对 作变换
作变换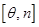 得
得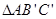 ,使点
,使点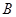 、
、 、
、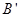 在同一直线上,且四边形
在同一直线上,且四边形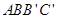 为平行四边形,求
为平行四边形,求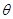 和
和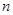 的值.
的值.
为了反映长江水位变化情况,你认为选择什么样的统计图比较好? 为什么?
一所中学准备搬迁到新校舍,在迁校舍之前就该校300名学生如何到校舍进行了一次调查,并得到如下数据:
| 步行 |
60人 |
| 骑自行车 |
100人 |
| 坐公共汽车 |
130人 |
| 其他 |
10人 |
请将上面的数据制成扇形统计图,根据你所制作的统计图,能得到什么结论? 说说你的理由.
(1)由图中提供信息:乒乓球、排球、足球、篮球4项球类活动中,哪一类球类运动能够获得全班近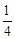 的支持率?
的支持率?
(2)若全班人数为50人,体育委员组织一次排球比赛,估计会有多少人积极参加比赛?
全班约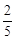 是男生,约
是男生,约 是女生,请根据所给数据完成扇形统计图.
是女生,请根据所给数据完成扇形统计图.
某人将20000元钱分成两部分,按两种不同方式存入银行,其中10000元按活期方式存一年,另10000元按定期存一年,一年后共取回21044元,又已知定期一年存款约利率为0.63%,求活期存款月利率是多少?