(本小题满分12分)已知椭圆C: 过点
过点
 ,离心率为
,离心率为 ,点
,点 分别为其左右焦点.
分别为其左右焦点.
(1)求椭圆C的标准方程;
(2)若 上存在两个点
上存在两个点 ,椭圆上有两个点
,椭圆上有两个点 满足,
满足, 三点共线,
三点共线, 三点共线,且
三点共线,且 .求四边形
.求四边形 面积的最小值.
面积的最小值.
已知函数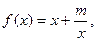 且函数
且函数 的图象经过点(1,2).
的图象经过点(1,2).
(1)求m的值;(2)证明函数 在(1,
在(1,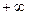 )上是增函数.
)上是增函数.
已知定义在实数集R上的奇函数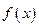 有最小正周期2,且当
有最小正周期2,且当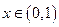 时,
时,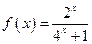 .
.
(1)求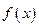 在
在 上的解析式;
上的解析式;
(2)试判断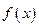 在
在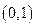 上的单调性,并证明;
上的单调性,并证明;
(3)是否存在实数 ,使方程
,使方程 在R上有解?若存在,求出
在R上有解?若存在,求出 的范围.若不存在,说明理由.
的范围.若不存在,说明理由.
(1)化简求值: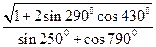 ;
;
(2)求函数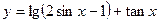 的定义域.
的定义域.
已知函数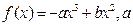 、
、 .
.
(1)讨论函数 的奇偶性(只写结论,不要求证明);
的奇偶性(只写结论,不要求证明);
(2)在构成函数 的映射
的映射 中,当输入值为
中,当输入值为 和2时分别对应的输出值为
和2时分别对应的输出值为 和
和 ,求
,求 、
、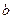 的值;
的值;
(3)在(2)的条件下,求函数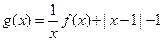 (
(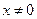 )的最大值.
)的最大值.
定义在 上的函数
上的函数 满足
满足 且当
且当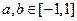 时,
时,
都有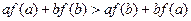 ;
;
(1)判断 在
在 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
(2)若 是奇函数, 不等式
是奇函数, 不等式 对所有的
对所有的 恒成立,
恒成立,
求 的取值范围.
的取值范围.