（本小题满分12分）某大型企业一天中不同时刻的用电量
（单位：万千瓦时）关于时间
（
，单位：小时）的函数
近似地满足
，下图是该企业一天中在0点至12点时间段用电量与时间的大致图象．
（Ⅰ）根据图象，求
，
，
，
的值；
（Ⅱ）若某日的供电量
（万千瓦时）与时间（小时）近似满足函数关系式
（
）．当该日内供电量小于该企业的用电量时，企业就必须停产．请用二分法计算该企业当日停产的大致时刻（精确度0.1）.
参考数据:
| （时） |
10 |
11 |
12 |
11.5 |
11.25 |
11.75 |
11.625 |
11.6875 |
 （万千瓦时） |
2．25 |
2.433 |
2.5 |
2.48 |
2.462 |
2.496 |
2.490 |
2.493 |
 （万千瓦时） |
5 |
3.5 |
2 |
2.75 |
3. 125 |
2.375 |
2.563 |
2.469 |
平面直角坐标系中，直线
的参数方程是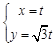
，以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，已知曲线C的极坐标方程为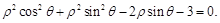
（1）求直线的极坐标方程
（2）若直线与曲线C相交于A,B两点，求|AB|
设矩阵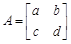
，矩阵A属于特征值
的一个特征向量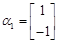
，属于特征值
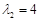的一个特征向量
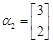，求
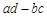的值
（本小题满分为16分）已知函数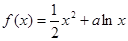
．
（1）若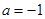
，求函数
的极值，并指出极大值还是极小值；
（2）若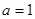
，求函数在
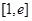上的最值；
（3）若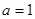，求证：在区间
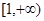上，函数的图象在
的图象下方．
（本小题满分为16分）设A，B分别为椭圆
的左、右顶点，椭圆的长轴长为
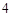，且点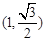
在该椭圆上．
（1）求椭圆的方程；
（2）设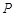
为直线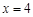
上不同于点
的任意一点，若直线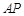
与椭圆相交于异于
的点
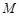，证明：△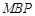
为钝角三角形．
（本小题满分为16分）为了保护环境，发展低碳经济，某单位在国家科研部门的支持下，进行技术攻关，新上了把二氧化碳处理转化为一种可利用的化工产品的项目，经测算，该项目月处理成本y（元）与月处理量x（吨）之间的函数关系可近似地表示为：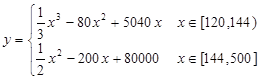
，且每处理一吨二氧化碳得到可利用的化工产品价值为200元，若该项目不获利，国家将给予补偿．
（1）当x∈[200,300]时，判断该项目能否获利？如果获利，求出最大利润；如果不获利，则国家每月至少需要补贴多少元才能使该项目不亏损？
（2）该项目每月处理量为多少吨时，才能使每吨的平均处理成本最低？