1932年美国物理学家劳伦斯发明了回旋加速器，巧妙地利用带电粒子在磁场中的运动特点，解决了粒子的加速问题。现在回旋加速器被广泛应用于科学研究和医学设备中。
某型号的回旋加速器的工作原理如图甲所示，图乙为俯视图。回旋加速器的核心部分为D形盒，D形盒装在真空容器中，整个装置放在电磁铁两极之间的磁场中，磁场可以认为是匀强磁场，且与D形盒盒面垂直。两盒间狭缝很小，带电粒子穿过的时间可以忽略不计。质子从粒子源A处进入加速电场的初速度不计，从静止开始加速到出口处所需的时间为t。已知磁场的磁感应强度为B，质子质量为m、电荷量为+q，加速器接一定频率高频交流电源，其电压为U。不考虑相对论效应和重力作用。求：
（1）质子第1次经过狭缝被加速后进入D形盒运动轨道的半径r1；
（2）D形盒半径为R；
（3）试推理说明：质子在回旋加速器中运动时，随轨道半径r的增大，同一盒中相邻轨道半径之差
是增大、减小还是不变?
（附加题）钚的放射性同位素
静止时衰变为铀核激发态
和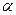
粒子，而铀核激发态立即衰变为铀核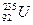
，并放出能量为
的
光子。已知：
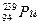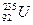、和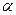粒子的质量分别为
、
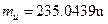和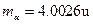
（1）写出衰变方程；
（2）已知衰变放出的光子的动量可忽略，求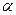粒子的动能。
如图所示，一质量为M的物块静止在桌面边缘，桌面离水平地面的高度为h。一质量为m的子弹以水平速度v0射入物块后，以水平速度v0/2射出。重力加速度为g。求
（1）子弹穿过物块后物块的速度V；
（2）此过程中系统损失的机械能；
（3）此后物块落地点离桌面边缘的水平距离。
如图所示，小车A、B的质量均为m，小车B静止于水平轨道上，其左端固定一根轻弹簧，小车A从高出水平轨道h处由静止开始沿曲轨道滑下，在水平轨道上与小车B发生相互作用．轨道是光滑的．求：
（1）A车沿曲轨道刚滑到水平轨道时的速度大小v0；
（2）弹簧的弹性势能最大时A车的速度v和弹簧的弹性势能Ep 。
天然放射性铀（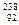
U）发生衰变后产生钍（
Th）和另一种原子核。
（1）请写出衰变方程；
（2）若衰变前铀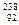（U）核的速度为v，衰变产生的钍（Th）核速度为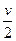
，且与铀核速度方向相同，求产生的另一种新核的速度。
分别用λ和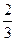
λ的单色光照射同一金属，发出的光电子的最大初动能之比为1∶2，以h表示普朗克常量，c表示真空中的光速，则此金属板的逸出功是多大？